Перш ніж приступити до рішення прикладів і завдань, обов'язково ознайомтеся з теоретичною частиною уроку
РІШЕННЯ ЗАВДАНЬ ЗА ДОПОМОГОЮ ВЕКТОРІВ
або
ВІДЕО УРОК
1. На рисунку зображено
квадрат ABCD.
Який з векторів дорівнює різниці векторів 2. На рисунку зображено ромб АВСD, у якому
АВ = 4 см,
4. На сторонах BC і CD паралелограма АВСD позначено відповідно точки E і FК так, що
BE : EC = 3 : 4,
Виразіть вектор
через вектори 5. Визначте вид чотирикутника АВСD, якщо а) трапеція;
6. Сторона правильного шестикутника ABCDEF дорівнює 1. Обчислить скалярній добуток
а) 0,8;
7. На сторонах АВ і ВС паралелограма АВСD позначено відповідно точки М і К так, що
АМ : МВ = 1 : 3,
Виразіть вектор
через вектори
8. На стороні AD паралелограма АВСD позначено точку K так, що
AK : KD = 1 : 3.
Виразіть вектор
через вектори де 9. Визначте вид чотирикутника АВСD, якщо а) трапеція;
10. На рисунку зображено квадрат ABCD.
Який з векторів дорівнює сумі векторів 11. Відрізок DE – середня лінія трикутника АВС, зображеного на рисунку. Яка з рівностей є правильною ? 12. Знайдіть довжину діагоналі АС паралелограма ABCD, якщо
А (2; –6; 0),
а) √͞͞͞͞͞31;
Який з векторів дорівнює різниці векторів 2. На рисунку зображено ромб АВСD, у якому
АВ = 4 см,
б) 5 см2;
в) 8 см2;
г) 10 см2.
б) 1;
в) 1,1;
г) 1,4.
4. На сторонах BC і CD паралелограма АВСD позначено відповідно точки E і FК так, що
BE : EC = 3 : 4,
CF
: FD = 1 : 3.
Виразіть вектор
через вектори 5. Визначте вид чотирикутника АВСD, якщо а) трапеція;
б) ромб;
в)
прямокутник;
г) паралелограм.
6. Сторона правильного шестикутника ABCDEF дорівнює 1. Обчислить скалярній добуток
а) 0,8;
б) 0,5;
в) 1,2;
г) 1,5.
7. На сторонах АВ і ВС паралелограма АВСD позначено відповідно точки М і К так, що
АМ : МВ = 1 : 3,
ВК : КС = 2 : 3.
Виразіть вектор
8. На стороні AD паралелограма АВСD позначено точку K так, що
AK : KD = 1 : 3.
Виразіть вектор
через вектори де 9. Визначте вид чотирикутника АВСD, якщо а) трапеція;
б) ромб;
в)
прямокутник;
г) паралелограм.
10. На рисунку зображено квадрат ABCD.
Який з векторів дорівнює сумі векторів 11. Відрізок DE – середня лінія трикутника АВС, зображеного на рисунку. Яка з рівностей є правильною ? 12. Знайдіть довжину діагоналі АС паралелограма ABCD, якщо
А (2; –6; 0),
В (–4;
8; 2),
D (0;
–12; 0).
а) √͞͞͞͞͞31;
б) √͞͞͞͞͞33;
в) 2√͞͞͞͞͞31;
г) 2√͞͞͞͞͞33.Завдання до уроку 7




















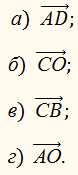


Комментариев нет:
Отправить комментарий