ВИДЕО УРОК
Розглянемо приклади графічного рішення простих тригонометричних нерівностей, тобто нерівностей виду:
f(x) ˃ a,
f(x) < a
де f(x) –
одна з тригонометричних функцій.
Графічна інтерпретація рішень нерівностей виду
sin х ˃ а,
sin х < а,
cos х ˃ а,
cos х < а,
tg х ˃ а,
tg х < а,
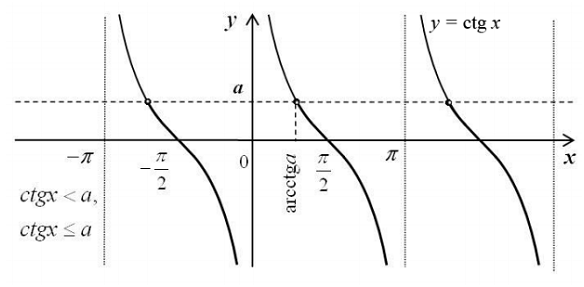
ctg х ˃ а,
ctg х < а,
Вирішити
графічно нерівність:
sin х ˃ 0.
РОЗВ'ЯЗАННЯ:
Побудуємо
графік функції
у = sin х
і
виберемо на осі х
значення аргументу х, яким відповідають точки графіку,
осі х,
що лежать вище. Одним з проміжків, що містять такі точки осі х,
є інтервал
(0; π), (дивіться малюнок),
у = sin х
кожен
з них виходить з (0; π) зрушенням по осі х на
2πk,
де k ∈ Z.
Таким
чином, рішенням заданої нерівності служить об'єднання інтервалів виду
(0 + 2πk; π
+ 2πk), тобто
(2πk; π + 2πk), k
∈ Z.
Це
можна записати так:
2πk < x < π + 2πk),
k ∈ Z.
ВІДПОВІДЬ:
2πk < x < π + 2πk),
k ∈ Z
ПРИКЛАД:
Вирішити
графічно нерівність:
соs х < 1/2.
РОЗВ'ЯЗАННЯ:
Побудуємо
графік функції
у = соs х
і
проведемо пряму
у =
1/2.
Нас
цікавлять ті значення аргументу х, яким відповідають точки графіку,
що лежать нижче прямої
у =
1/2.
Одним
з потрібних нам проміжків є інтервал
у = соs х,
запишемо
відповідь.
ВІДПОВІДЬ:
π/3
+ 2πk < x < 5π/3 + 2πk, k ∈ Z
ПРИКЛАД:
Вирішити
графічно нерівність:
tg х ≥ –1.
РОЗВ'ЯЗАННЯ:
Побудуємо
графік функції
у = tg х
і
проведемо пряму
у =
–1.
Нас
цікавлять ті значення х, яким відповідають точки графіку,
що лежать не нижче прямої
[–π/4; π/2),
А
всього таких проміжків буде нескінченне багато, причому в силу періодичності
функції
у = tg х
кожен
виходить з
[–π/4; π/2)
зрушенням
по осі х на πk, де k ∈ Z. Це дозволяє записати рішення
таким чином.
ВІДПОВІДЬ:
–π/4 + πk ≤ x < π/2 + πk, k ∈ Z
ПРИКЛАД:
Вирішити
графічно нерівність:
cos х – 3х
+ 1 ≥ 0.
РОЗВ'ЯЗАННЯ:
При
рішенні нерівності графічним способом необхідно як можна точніше побудувати
графіки функцій.
Перетворимо
цю нерівність до виду:
cos х ≥ 3х
– 1.
Побудуємо
в одній системі координат графіки функцій
у = cos х,
х ≈ 0,6 і
у
≈ 0,8.
На
проміжку (–∞; 0,6)
точки графіку
у = 3х – 1
нижче
точок графіку
у = cos х.
А
при х ≈ 0,6 значення
функцій співпадають. Тому
cos х ≥ 3х – 1
при х ≤ 0,6.
ВІДПОВІДЬ:
х
∈ (–∞; 0,6].
ПРИКЛАД:
Вирішити
графічно нерівність:
sin х < 2х – 1.
РОЗВ'ЯЗАННЯ:
Побудуємо
в одній системі координат графіки функцій
у = sin х,
А(х ≈ 0,9; у ≈ 0,8).
На проміжку (0,9; +∞)
точки графіку
у = 2х – 1
вище за точки графіку
у = sin х.
Значить
sin х < 2х – 1
при
х ˃ 0,9.
ПРИКЛАД:
Вирішити
графічно нерівність:
соs х – х2
– 2х – 1 ≥ 0.
РОЗВ'ЯЗАННЯ:
Перетворимо
цю нерівність до виду:
соs х ≥ х2
+ 2х + 1.
Побудуємо
в одній системі координат графіки функцій
у = соs х,
Графіки функцій перетинаються в
точках
А(0; 1)
и В(х ≈ –1,4; у ≈ 0,2).
На проміжку [–1,4; 0]
точки графіку функції
у = х2 + 2х + 1
нижче точок графіку
у = соs х.
значить,
соs х ≥ х2
+ 2х + 1
при
–1,4 ≤ х ≤ 0.
ВІДПОВІДЬ: х ∈ [–1,4; 0]
ПРИКЛАД:
Вирішити
графічно нерівність:
sin х ≤
1/3.
РОЗВ'ЯЗАННЯ:
Побудуємо
в одній системі координат графіки функцій
у = sin х,
А(–3,481;
0,333)
і В(3,4; 0,333).
На проміжку [–3,481; 3,4] точки графіку функції
у = sin х
нижче точок графіку
у = 1/3.
значить,
sin х ≤
1/3
при
–3,481 ≤ х ≤ 3,4,
або
–π – arcsin 1/3 ≤ х ≤ arcsin 1/3.
ПРИКЛАД:
Таким
чином, одним із проміжків розв’язку заданої нерівності є
2π/3
≤ х < π.
Добавляємо
періодичність котангенса та записуємо множину розв’язків нерівності.
x ∈
[2π/3 + πk; π + πk) k
∈ Z.
ПРИКЛАД:
Якщо нерівність нестрога, то точки перетину включаємо в розв’язок і дістаємо проміжок.Знайдемо абсциси точок х1 і х2 (х1 < х2) – перетину графіків зазначених функцій:Запишемо відповідь, врахувавши період функції у = sin х.
Отже,
розв’язком нерівності є множина значень
x ∈
(–5π/3 + 2πk; π/4 + 2πk) k
∈ Z.
ПРИКЛАД:
x ∈
(–π/6
+ 2πk; π/6 + 2πk) k
∈ Z.
ПРИКЛАД:
Вирішити
графічно нерівність:
tg x < √͞͞͞͞͞3.
РОЗВ'ЯЗАННЯ:
Побудуємо
в декартовій системі координат графіки функцій
у
= tg x,
у = √͞͞͞͞͞3
та
виділимо проміжки, на яких графік функції
у
= tg х
розташований нижче від графіка прямої
Знайдемо
через арктангенс абсцису точки х0 –
перетину графіків зазначених функцій, яка є кінцем одного з проміжків, на якому
виконується задана нерівність
х0 = arctg √͞͞͞͞͞3
= π/3.
Іншим
кінцем цього проміжку є точка – π/2, у
якій функція у = tg x
невизначена (розрив
II роду).
Таким
чином, одним із проміжків розв’язку заданої нерівності є
–π/2 < х
< π/3.
Враховуючи,
що період тангенса рівний π
записуємо загальний розв’язок нерівності:
- Урок 1. Найпростіші тригонометричні рівняння
- Урок 2. Методи розв'язування тригонометричних рівнянь з функціями одного аргументу
- Урок 3. Тригонометричні рівняння з функціями різних аргументів
- Урок 4. Графічні методи розв'язання тригонометричних рівнянь
- Урок 5. Системи тригонометричних рівнянь
- Урок 6. Тригонометричні нерівності



































Комментариев нет:
Отправить комментарий