Перш ніж приступити до рішення прикладів і завдань, обов'язково ознайомтеся з теоретичною частиною уроку
ПЕРЕСТАНОВКИабо
ВИДЕО УРОК
1. Скількома
способами можна розкласти в один ряд чотири різні монети ?
а) 20;
б) 28;
в) 24;
г) 16.
г) 16.
2. Скільки семицифрових чисел, кратних 5, можна скласти з цифр
3, 4, 5, 6, 7, 8, 9
Так щоб цифри в числі не повторювались ?
а) 720;
б) 705;
в) 732;
г) 724.
г) 724.
3. Скількома способами можна розставити на полиці п'ять різних книг ?
а) 140;
б) 128;
в) 110;
г) 120.
г) 120.
4. В змаганні брало участь 4 команди. Кожна команда грала з усіма іншими командами. Скільки всього ігор було зіграно ?
а) 18;
б) 24;
в) 28;
г) 12.
г) 12.
5. Скількома способами можна в садочку поставити групу з 15 дітей в ряд ?
а) 13!;
б) 17!;
в) 15!;
г) 14!.
г) 14!.
6. На книжковій полиці розміщують 20 томів енциклопедії. Скількома способами їх можна розмістити так, щоб томи 12 і 13 не стояли поруч ?
а) 18! × 20!;
б) 17! × 20!;
в) 17! × 19!;
г) 18! × 19!.
7. Обчислити:
б) 131;
в) 138;
г) 135.
г) 135.
8. Обчислити:
б) (k
– 3)(k – 2)k;
в) (k
– 1)k;
г) (k
– 2)(k – 1).
9. Множина М складається з трьох елементів:
Знайти Р3.
10. Скільки п'ятизначних чисел, не кратних п'яти,
можна скласти з цифр
9. Множина М складається з трьох елементів:
3, 4, 5, 6, 7
без повторень цифр у кожному з них ?
а) 92;
б) 96;
б) 96;
в) 98;
г) 102.
г) 102.
11. Візьмемо букви Б, А, Р.
Скільки наборів вийде, якщо букви в наборі не повторюються ?
а) 7;
б) 8;
б) 8;
в) 6;
г) 4.
г) 4.
12. Візьмемо букви
Б, А, Р.
Скільки наборів вийде, якщо буква А повторюється двічі ?
а) 12;
б) 16;
б) 16;
в) 11;
г) 14.
г) 14.
Завдання до уроку 3
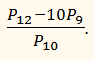
Комментариев нет:
Отправить комментарий