Перш ніж приступити до рішення прикладів і завдань, обов'язково ознайомтеся з теоретичною частиною уроку
ЗАСТОСУВАННЯ ПОХІДНОЇ ДО ДОСЛІДЖЕННЯ ФУНКЦІЙ
або
ВИДЕО УРОК
1. Чому дорівнює кутовий
коефіцієнт дотичної до графіка функції
у точці з абсцисою
х0 = 7,5 ?
а) 3/2;
2. Функція у = f(x) визначена на проміжку [a; b] і має похідну в кожній точці області визначення. На рисунку зображено графік функції у = f ' (x).
Скільки проміжків спадання має функція у = f(x) ?
а) 1;
3. Функція у = f(x) визначена на проміжку [–4; 4] і має похідну в кожній точці області визначення. На рисунку зображено графік функції у = f ' (x).
Знайдіть точки мінімуму функції у = f(x).
а) –3;
4. Функція у = f(x) визначена на проміжку [–8; 3] і має похідну в кожній точці області визначення. На рисунку зображено графік її похідної у = f ' (x).
Укажіть точки мінімуму функції у = f(x).
а) 0;
5. На рисунку зображено графік функції у = f (x).
Користуючись графіком, порівняйте
f ' (x1) і f ' (x2).
а) f ' (x1) < f ' (x2);
6. Прямі а і b, зображені на рисунку, паралельні, причому пряма а є дотичною до графіка функції у = f (x) у точці з абсцисою х0, а рівняння прямої b має вигляд
2х – у + 3 = 0.
Знайдіть f ' (x0)
а) –1;
7. На рисунку зображено графік функції у = f (x).
Укажіть правильну
подвійну нерівність.
а) f ' (–2) < f ' (1) < f ' (2);
8. Функція у = f(x), графік якої зображено на рисунку, визначена на проміжку [–3; 3].
Укажіть множину значень аргументу функції, при
яких f ' (x) ˃ 0.
а) (–2; 0) ∪ (0; 3);
9. Функція у = f(x) визначена на проміжку [–8; 3] і має похідну в кожній точці області визначення. На рисунку зображено графік функції у = f ' (x).
Визначте проміжки зростання функції у = f(x).
а) [–8; –4] і [0; 3];
10. Функція у = f(x) визначена на проміжку [a; b] і має похідну в кожній точці області визначення. На рисунку зображено графік функції у = f ' (x).
Скільки
точок екстремуму має функція у = f(x) ?
а) жодної точки;
11. Функція у = f(x) визначена на проміжку [a; b] і має похідну в кожній точці області визначення. На рисунку зображено графік функції у = f ' (x).
Скільки
проміжків зростання має функція у = f(x) ?
а) 2;
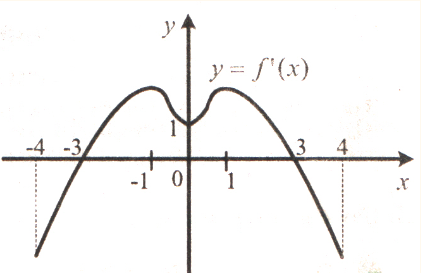
12. Функція у = f(x) визначена на проміжку [–4; 4] і має похідну в кожній точці області визначення. На рисунку зображено графік функції у = f ' (x).
Знайдіть точки максимуму функції у = f(x).
а) 0;
х0 = 7,5 ?
а) 3/2;
б) 1/2;
в) 1/4;
г) 3/4.
2. Функція у = f(x) визначена на проміжку [a; b] і має похідну в кожній точці області визначення. На рисунку зображено графік функції у = f ' (x).
а) 1;
б) 2;
в) 3;
г) встановити неможливо.
3. Функція у = f(x) визначена на проміжку [–4; 4] і має похідну в кожній точці області визначення. На рисунку зображено графік функції у = f ' (x).
а) –3;
б) –1; 1;
в) 0;
г) 3.
4. Функція у = f(x) визначена на проміжку [–8; 3] і має похідну в кожній точці області визначення. На рисунку зображено графік її похідної у = f ' (x).
а) 0;
б) –4;
в) –6; –3; 2;
г) –6; 2.
5. На рисунку зображено графік функції у = f (x).
f ' (x1) і f ' (x2).
а) f ' (x1) < f ' (x2);
б) f
'
(x1) = f ' (x2);
в) f
'
(x1) ˃ f ' (x2);
г) порівняти
неможливо.
6. Прямі а і b, зображені на рисунку, паралельні, причому пряма а є дотичною до графіка функції у = f (x) у точці з абсцисою х0, а рівняння прямої b має вигляд
2х – у + 3 = 0.
а) –1;
б) 2;
в) 3;
г) встановити
неможливо.
7. На рисунку зображено графік функції у = f (x).
а) f ' (–2) < f ' (1) < f ' (2);
б) f
'
(2) < f ' (1) < f ' (–2);
в) f
'
(1) < f ' (–2) < f ' (2);
г) f
'
(1) < f ' (2) < f ' (–2).
8. Функція у = f(x), графік якої зображено на рисунку, визначена на проміжку [–3; 3].
а) (–2; 0) ∪ (0; 3);
б) [–3; –1] ∪ [0; 2];
в) [–2; 3];
г) (–1; 0) ∪ (2; 3].
9. Функція у = f(x) визначена на проміжку [–8; 3] і має похідну в кожній точці області визначення. На рисунку зображено графік функції у = f ' (x).
а) [–8; –4] і [0; 3];
б) [–6; –3] і [2; 3];
в) [–3; 1];
г) визначити
неможливо.
10. Функція у = f(x) визначена на проміжку [a; b] і має похідну в кожній точці області визначення. На рисунку зображено графік функції у = f ' (x).
а) жодної точки;
б) 6 точок;
в) 3 точки;
г) 4 точки.
11. Функція у = f(x) визначена на проміжку [a; b] і має похідну в кожній точці області визначення. На рисунку зображено графік функції у = f ' (x).
а) 2;
б) 3;
в) 4;
г) не
можна встановити.
12. Функція у = f(x) визначена на проміжку [–4; 4] і має похідну в кожній точці області визначення. На рисунку зображено графік функції у = f ' (x).
а) 0;
б) –1, 1;
в) –3;
г) 3.Завдання до уроку 7
Комментариев нет:
Отправить комментарий