Перш ніж приступити до рішення прикладів і завдань, обов'язково ознайомтеся з теоретичною частиною уроку
КОНУС
або
ВІДЕОУРОК
1. Висота конуса дорівнює 14 см, а кут при вершині осьового перерізу – 120°. Знайдіть радіус основи конуса.
а) 14√͞͞͞͞͞3 см;
б) 7√͞͞͞͞͞2 см;
в) 14
см;
г) 7 см.
2.
Обчисліть площу бічної поверхні конуса, діаметр основи якого дорівнює 12 см,
а твірна – 17 см.
а) 102π см2;
б) 204π см2;
в) 34π см2;
г) 68π см2.
3.
Обчисліть площу бічної поверхні конуса, радіус основи якого дорівнює 9 см,
а твірна – 16 см.
а) 144π см2;
б) 72π см2;
в) 72 см2;
г) 48π см2.
4. Кут між
твірною і площиною основи конуса дорівнює
60°,
висота конуса – 9√͞͞͞͞͞3 см.
Знайдіть твірну конуса.
а) 13,5 см;
б) 18√͞͞͞͞͞3 см;
в) 9 см;
г) 18 см.
5. Обчисліть
площу бічної поверхні конуса, радіус основи якого дорівнює 8 см,
а твірна – 12 см.
а) 32π см2;
б) 48π см2;
в) 48 см2;
г) 96π см2.
6.
Обчисліть площу бічної поверхні конуса, твірна якого дорівнює 8 см,
а радіус основи – 10 см.
а) 40π см2;
б) 80π см2;
в) 40 см2;
г) 80 см2.
7. Кут між твірною і
площиною основи конуса дорівнює 30°,
радіус основи конуса – 6√͞͞͞͞͞3 см.
Знайдіть висоту конуса.
а) 6 см;
б) 18 см;
в) 12√͞͞͞͞͞3
см;
г) 3√͞͞͞͞͞3
см.
8. Радіус основи конуса
дорівнює 5 см,
а його висота – 12 см.
Знайдіть площу бічної поверхні конуса.
а) 60π см2;
б) 70π
см2;
в) 65π см2;
г) 62π см2.
9. Осьовий переріз конуса
– рівнобедрений прямокутний трикутник, висота якого, проведена до основи,
дорівнює 10 см.
Знайдіть площу бічної поверхні конуса.
а) 90π(3 + √͞͞͞͞͞2
) см2;
б) 100π(1 + √͞͞͞͞͞2
) см2;
в) 100π(1 + √͞͞͞͞͞3
) см2;
г) 120π(1 + √͞͞͞͞͞2
) см2.
10. Висота конуса дорівнює Н,
а кут при вершині осьового перерізу – 2α.
Знайдіть площу бічної поверхні конуса.
а) 60°;
б) 30°;
б) 30°;
в) 90°;
г) 45°.
г) 45°.
12. Через дві твірні конуса, кут між якими
дорівнює φ,
проведено переріз. Знайдіть площу цього перерізу, якщо висота конуса
дорівнює h і утворює з його твірною кут α.
Завдання до уроку 13
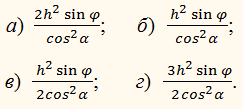
Комментариев нет:
Отправить комментарий