Урок 11. Циліндр

суббота, 13 января 2018 г.

Урок 11. Циліндр

ВІДЕОУРОК

Циліндричною поверхнею називається поверхня, яка утворюється рухом прямої АВ, що зберігає один і той самий напрям і перетинає дану лінію СD.

Пряма АВ називається твірною, а лінія СD – напрямною.

Якщо за напрямну циліндричної поверхні взяти коло, площина якого перпендикулярна до твірної, то така поверхня називається круговою циліндричною.

Циліндром називається тіло, обмежене циліндричною поверхнею із замкнутою напрямною і двома паралельними площинами, які перетинають твірні.

Частина циліндричної поверхні, що лежить між паралельними площинами, називається бічною поверхнею циліндра, а частини площин, які відтинає ця поверхня, – основами циліндра. Віддаль між площинами основ називається висотою циліндра.

Прямий круговий циліндр.

Прямім круговим циліндром називається тіло, обмежене круговою циліндричною поверхнею і двома паралельними площинами, перпендикулярними до твірної.

В елементарній геометрії звичайно розглядають тільки прямий круговий циліндр, який далі будемо називати просто циліндром.

Основами прямого кругового циліндра є круги радіуса R, а висота дорівнює твірній циліндра:

Н = АВ = ОО₁.

Циліндр можна також одержати обертанням прямокутника АОО₁В навколо однієї з його сторін.

Сторона прямокутника ОО₁, навколо якої відбувається обертання, називається віссю циліндра, а перпендикулярна до неї сторона
ОА = R – радіусом циліндра.

Радіус циліндра дорівнює радіусу його основ.

Бічна і повна поверхні циліндра.

За бічну поверхню циліндра приймають границю, до якої наближається бічна поверхня вписаної в цей циліндр (або описаної навколо нього) правильної призми, коли число граней цієї призми необмежено збільшується, а довжина основи кожної з її граней наближається до нуля.

Бічна поверхня циліндра дорівнює добутку довжини кола основи на висоту циліндра:

S_бічн = 2πRH,

де R – радіус основи циліндра, а H – його висота.

Повна поверхня циліндра дорівнює сумі бічної поверхні і площ його основ:

S_повн = 2πR(H + R).

Бічна поверхня циліндра – дорівнює добутку висоти тіла на довжину кола, радіус якого є перпендикуляром, поставленим до твірної з її середини до перетину з віссю.

Бічна поверхня циліндра дорівнює

S_бічн = 2π × ОА × О₁О₂.

Розгортка циліндра.

Якщо поверхню циліндра розрізати по твірній і колах основ і розгорнути її так, щоб бічна поверхня разом з основами лежала в одній площині, то на цій площині одержимо фігуру, яка називається розгорткою циліндра.

Розгортка циліндра складається з прямокутника АВСD, сторони якого

АВ = Н і СВ = 2πR,

і двох кругів (основ циліндра) О і О₁.

ЗАДАЧА:

Висота циліндра 6 дм, радіус основи – 5 дм. Кінці даного відрізка лежать на колах обох основ; довжина його дорівнює 10 дм. Знайти найкоротшу віддаль між даним відрізком і віссю.

РОЗВ'ЯЗАННЯ:

У даному циліндрі

АМ = 6 дм, АО = 5 дм

і відрізок

МN = 10 см.

Знайти віддаль між відрізком МN і віссю циліндра ОО₁.

МN і ОО₁ – мимобіжні прямі. Проведемо площину МАN через пряму МN паралельно до осі ОО₁; тоді віддаль від будь-якої точки осі ОО₁ до проведеної площини буде шуканою. З прямокутного ⊿МАN дістанемо:

З прямокутного ⊿ABO

У цьому випадку

CD = BO = 3 дм.

ВІДПОВІДЬ: 3 дм.

ЗАДАЧА:

В циліндрі площа основи дорівнює Q, а площа осьового перерізу S. Визначити повну поверхню циліндра.

РОЗВ'ЯЗАННЯ:

В циліндрі

S_осн = Q і S_АВСD = S.

Знайти S_повн циліндра.

Позначимо

AO = R і AD = H, тоді

S_повн = 2πR(H + R).

За умовою задачі

2RH = S, πR² = Q,

звідки

Тоді

ВІДПОВІДЬ: πS + 2Q

ЗАДАЧА:

Бічна поверхня циліндра вдвічі більша за суму площ його основ. Знайти кут між діагоналлю осьового перерізу і площиною основи циліндра.

РОЗВ'ЯЗАННЯ:

За умовою задачі

S_бічн = 4S_осн.

Знайти ∠ AСD = α.

Відомо, що

S_бічн = 2πRH, а

S_осн = πR², тоді

2πRH = 4πR²

і, отже,

H = 2R,

Тобто прямокутний ⊿ADC – рівнобедрений,

AD = DC = 2R.

Шуканий кут α = 45°.

ВІДПОВІДЬ: 45°

Вирішення стереометричних задач за допомогою тригонометрії.

ЗАДАЧА:

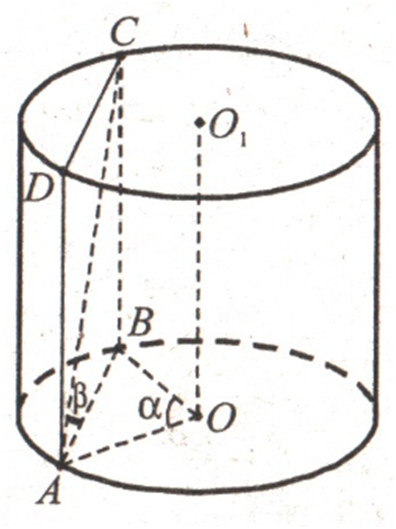
У циліндрі паралельно його осі проведено площину, що перетинає нижню основу циліндра по хорді, яку видно з центра цієї основи під кутом α. Діагональ утвореного перерізу нахилена до площини основи під кутом β. Знайдіть площу бічної поверхні циліндра, якщо площа його основи дорівнює S.

РОЗВ'ЯЗАННЯ:

Нехай циліндр з віссю ОО₁ перетнуто площиною АВС, яка паралельна осі.

У перерізі утвориться прямокутник АВСD. Ця площина перетинає нижню основу циліндра по хорді АВ. Тоді ∠ AОВ = α. АВ є проекцією діагоналі АС прямокутника на площину основи. Тому – кут нахилу діагоналі АС до площини основи. Тому ∠ САВ – кут нахилу діагоналі АС до площини основи. За умовою, ∠ САВ = β.

Одержимо πR² = S. Звідси
∠ АОВ – центральний кут, а будь-який вписаний у це коло кут, який спирається на дугу АВ, дорівнює ^𝛼/₂. Тоді за наслідком з теореми синусів
З ∆ CAB (∠ В = 90°):

ВІДПОВІДЬ: 4S sin ^𝛼/₂ tg β

ЗАДАЧА:

У циліндрі паралельно його осі проведено площину, що перетинає нижню основу циліндра по хорді, яку видно з центра цієї основи під кутом α. Знайдіть площу бічної поверхні циліндра, якщо площа утвореного перерізу дорівнює S.

РОЗВ'ЯЗАННЯ:

Заданий циліндр з віссю ОО₁, перетнуто площиною АВС, яка паралельна осі. У перерізі утвориться прямокутник АВСD, площа якого дорівнює S. Ця площина перетинає нижню основу циліндра по хорді АВ. Тоді ∠ АОВ = α. Проведемо ОК ⊥ АВ. Тоді

АВ = 2АК = 2АО sin ^𝛼/₂ = 2R sin ^𝛼/₂.

Тоді
ВІДПОВІДЬ:
Завдання до уроку 11

Інші уроки:

Уроки математики и физики для школьников и родителей

суббота, 13 января 2018 г.