Урок 22. Квадрат

понедельник, 1 декабря 2014 г.

Урок 22. Квадрат

ВІДЕОУРОК

Квадрат – прямокутник, у якого всі сторони рівні.

ABCD – квадрат,

AB = BC = CD = AD,

∠ A = ∠ B = ∠ C = ∠ D = 90°.

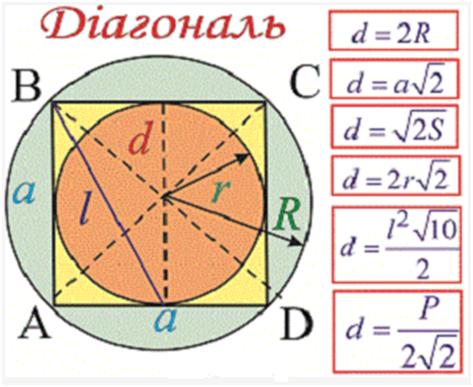
Властивості квадрата.

– усі сторони квадрата рівні;
– всі кути квадрата прямі;
– діагоналі квадрата рівні;
– діагоналі квадрата взаємно перпендикулярні;
– діагоналі квадрата точкою перетину діляться навпіл;
– діагоналі квадрата ділять кути квадрата навпіл;
– діагоналі квадрата ділять його на чотири рівні прямокутні рівнобедрені трикутники.
Формули для знаходження діагоналі квадрата.
ЗАДАЧА:

На стороні CD квадрата ABCD позначено точку К так, що

∠ AВК = 60°.

Знайдіть відрізок AК, якщо

ВС = √͞͞͞͞͞6 см.

РОЗВ’ЯЗАННЯ:

Накреслимо креслення:

ABCD – квадрат,

∠ AВК = 60°,

ВС = √͞͞͞͞͞6 см.

За умовою

∠ AВК = 60°, тоді

∠ КВС = 90° – 60° = 30°.

Розглянемо ∆ ВСК (∠ С = 90°).

Так як кут ∠ КВС = 30°, о проти кута 30° лежить катет, що дорівнює половині гіпотенузи, тобто ВК = 2СК. Позначимо

СК = х, тоді ВК = 2х.

За теоремою Піфагора запишемо:

ВК² = ВС² + СК²,

(2СК)² = ВС² + СК²,

3СК² = (√͞͞͞͞͞6)²,

СК² = 2, СК = √͞͞͞͞͞2 (см).

КD = СD – СК = (√͞͞͞͞͞6 – √͞͞͞͞͞2) (см).

Розглянемо ∆ АКD (∠ D = 90°).

АК² = АD² + КD² =

= (√͞͞͞͞͞6 )² + (√͞͞͞͞͞6 – √͞͞͞͞͞2)² =

= 6 + 6 – 2√͞͞͞͞͞12 + 2 =

= 14 – 4√͞͞͞͞͞3.

ЗАДАЧА:

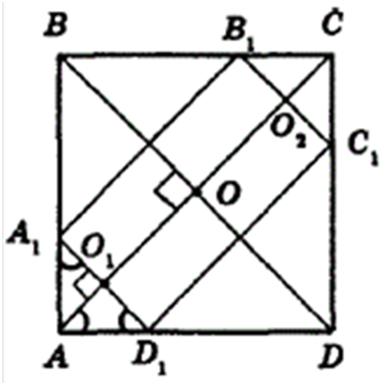
У квадрат вписано прямокутник так, що на кожній стороні квадрата знаходиться одна вершина прямокутника та сторони прямокутника паралельні діагоналям квадрата. Знайдіть сторони прямокутника, знаючи, що одна з них удвічі більша за іншу і що діагональ квадрата дорівнює 12 м.

РОЗВ’ЯЗАННЯ:

Накреслимо креслення.
∠ ВОА = 90° (діагоналі квадрата перетинаються під прямим кутом).

∠ ВОА = ∠ А₁О₁А = 90° (як відповідні кути для паралельних прямих ВD і А₁D, та січної АС).

АС – бісектриса, тому

∠ А₁АО₁ = ∠ О₁АD₁ =

= ¹/₂ ∠ А = 45°.

Значить,

∠ АА₁О₁ = ∠ АD₁О₁ = 45°.

∆ А₁АD₁ – рівнобедрений, оскільки АО₁ є висотою, бісектрисою, отже, і медіаною.

Значить

А₁О₁ = О₁D₁,

∆ АО₁D₁– рівнобедрений, тому

АО₁ = О₁D₁.

Так що

А₁О₁ = АО₁ = О₁D₁.

Нехай відрізок А₁О₁ = х м, тоді

А₁D₁ = 2х м і

А₁В₁ = 2А₁D₁ = 4 м.

Далі,

АС = АО₁ + О₁О₂ + О₂С =

= АО₁ + А₁В₁ + О₂С.

х + 4х + х = 12,

6х = 12 м, х = 2 м.

Тоді

А₁D₁ = 2х = 2 ∙ 2 = 4 (м).

А₁В₁ = 4х = 8 (м).

А₁D₁ = В₁С₁ = 4 (м),

А₁В₁ = D₁С₁ = 8 (м).

ВІДПОВІДЬ: 4 м, 8 м

ЗАДАЧА:

У рівнобедрений прямокутний трикутник вписаний квадрат так, що дві його вершини знаходяться на гіпотенузі, а дві інші – на катетах. Знайдіть сторону квадрата, якщо гіпотенуза дорівнює 3 м.

РОЗВ’ЯЗАННЯ:

Накреслимо креслення.
∆ АВС – прямокутний, рівнобедрений, тоді,

∠ АВС = ∠ АСВ =

= ¹/₂ (180° – 90°) = 45°.

∆ DКС – рівнобедрений, оскільки

∠ DКС = 90°, ∠ АСК = 45°,

тоді та ∠ КDС = 45°.

Значить DК = КС.

Аналогічно і ∆ ВLЕ – рівнобедрений і

ВЕ = LЕ,

LЕ = КD = ЕК – стороні квадрата.

Нехай ВЕ = х м. Тоді

ЕК = КС = х м,

ВС = ВЕ + ЕК + КС =

= 3х = 3 м,

х = 1 м.

Звідки ЕК = 1 м.

ВІДПОВІДЬ: 1 м

Периметр квадрата.

Насправді дуже часто доводиться вирішувати завдання визначення периметра квадрата.

Квадрат – це постать, що лежить в одній площині. Якщо виміряємо і складемо всі сторони квадрата, то отримаємо число, яке називається периметром даного квадрата. Якщо в квадраті позначимо сторону а, то периметр квадрата Р дорівнюватиме:

Знайти периметр квадрата – це означає обчислити суму сторін. Якщо периметр – це сума довжин усіх сторін фігури, то напівпериметр – сума двох сторін квадрата.

Формули для знаходження периметра квадрата.
ЗАДАЧА:

Сума діагоналей квадрата дорівнює 2√͞͞͞͞͞2. Знайдіть його периметр.

РОЗВ’ЯЗАННЯ:

Якщо сума діагоналей дорівнює 2√͞͞͞͞͞2, а діагоналі квадрата рівні, то одна діагональ дорівнює √͞͞͞͞͞2. Так як діагональ квадрата в √͞͞͞͞͞2 рази більша за сторону, то сторона дорівнює 1. Значить, периметр квадрата буде дорівнює 4.

ЗАДАЧА:

У рівнобедрений прямокутний трикутник вписано квадрат так, що вони мають спільний прямий кут. Знайдіть периметр квадрата, якщо катет трикутника дорівнює 4 см.

РОЗВ'ЯЗАННЯ:

Розглянемо ∆ ВРС і ∆ МСК.

Вони рівнобедрені, бо прямокутні з гострім кутом 45° (кути Р і К – кути рівнобедреного трикутника за умовою) і мають рівні сторони

РВ = ВС = СМ = МК.

Тому ∆ ВРС = ∆ МСК за двома катетами чи за катетом і гострім кутом. Отже, сторона квадрата дорівнює половині катета заданого рівнобедреного прямокутного трикутника. Периметр квадрата

АВСМ

2 × 4 = 8 (см).

ВІДПОВІДЬ: 8 см.

ЗАДАЧА:

Через вершини квадрата з периметром 8√͞͞͞͞͞2 см проведено прямі які паралельні його діагоналям. Обчисліть периметр утвореного чотирикутника.

РОЗВ’ЯЗАННЯ:

Накреслимо креслення.

Дано: квадрат KLMN, у якого сторона KL дорівнює

8√͞͞͞͞͞2 : 4 = 2√͞͞͞͞͞2 (см).

Розглянемо трикутник KBL. Він рівнобедрений та прямокутний, у якому

KL = 2√͞͞͞͞͞2 (см) – гіпотенуза.

Позначимо

КВ = ВL = х,

тоді за теоремою Піфагора, отримаємо:

х² + х² = (2√͞͞͞͞͞2)²,

Знайдемо х.

2х² = 8, х² = 4,

х = 2.

Це половина сторони чотирикутника, який є квадратом, отже, його периметр дорівнює:

2 ∙ 2 ∙ 4 = 16 (см).

ВІДПОВІДЬ: 16 см.

Завдання до уроку 22

Інші уроки:

Уроки математики и физики для школьников и родителей

понедельник, 1 декабря 2014 г.