ВІДЕОУРОК
Що таке сила ?
Сила - це фізичне явище, здатне
змінити форму матеріальних тіл, викликати їх рух, змінювати напрямок і
швидкість руху цих тіл або приводити тіло до стану спокою.
ПРИКЛАД:
Хлопці зліпили
сніговика, а хулігани його зруйнували. Виходить, що хулігани доклали до
сніговика свою силу, тим самим викликали зміну форми сніговика.
На дворі стояв
візок. Перехожий випадково зачепив її, і візок зрушив з місця. Виходить, що
перехожий застосував силу до візка і викликав рух.
Далі той же
перехожий зупинив візок, щоб він далеко не поїхав. Виходить, що перехожий
застосував силу, тим самим привів візок у стан спокою.
Сила є фізичною величиною – мірою на тіло інших тіл. Сила позначається
буквою F.
Що таке робота ?
Робота – це кількісна міра впливу сили на тіло. Робота залежить від
кількості сили, прикладеної на тіло та від напрямку цієї сили, а також від переміщення
даного тіла.
ПРИКЛАД:
Якщо ми
спробуємо зрушити шафу з місця, і вона зрушить, то можна сказати, що ми зробили
роботу, оскільки сила, яку ми доклали, призвела до того, що шафа здійснила
переміщення на деяку відстань.
Якщо ж ми,
наприклад, спробуємо штовхнути стіну, то стіна з місця не зрушить, а значить і
робота не буде виконана, оскільки сила була прикладена, але ця сила не
викликала жодного переміщення стіни.
Робота позначається великою латинською літерою А.
Спільна робота виникає, коли кілька людей (бригад, насосів тощо)
виконують одну й ту саму роботу разом, причому працюють з різними швидкостями.
У таких завданнях завжди присутні одні й самі величини, їх три:
Перша величина – це час, протягом
якого виконується та чи інша робота. Позначають час буквою t.
Друга величина – обсяг роботи, тобто
скільки зроблено деталей, налито води, зорано полів тощо. Позначають обсяг
роботи літерою А.
Третя величина – продуктивність. По суті, це
швидкість роботи.
Швидкість будь-якої роботи, тобто продуктивність, можна визначити, як
обсяг роботи, зробленої за якийсь час.
Продуктивністю називають роботу,
виконану за одиницю часу.
Під одиницею мається на увазі 1 час, 1 хв, 1 сек.
Позначають продуктивність літерою П.
Якщо відомі робота та час роботи, то можна знайти продуктивність.
Щоб знайти продуктивність, треба
виконану роботу поділити на час роботи.
Формула для продуктивності:
П = А : t.
ЗАДАЧА:
Два пекарі пекли булочки. Перший пекар випік 40 булочок за 10 хв, а другий 15 булочок за 5 хв. Як дізнатися, хто з пекарів працював швидше, перший чи другий ?
РОЗВ'ЯЗАННЯ:
Працював
швидше той, хто за одну хвилину випікає більше булочок. Говорять, що в нього
продуктивність більша. Знаючи правило чи формулу знаходження продуктивності,
можна визначити, скільки булочок посідає одну хвилину.
Знайдемо
продуктивність першого пекаря. Розділимо роботу, яку він виконав, на час, який
він витратив на неї. Виконана робота – це кількість випечених ним булочок,
тобто 40, а час – 10 хв.
40 : 10 = 4 булочки на хвилину.
Аналогічно
знайдемо продуктивність другого пекаря. Розділимо 15 на 5:
15 : 5 = 3 булочки на хвилину.
Перший пекар
за хвилину випікає більше булочок, ніж другий, отже його продуктивність вища.
Звідси робимо висновок, що працює він швидше за другого пекаря.
Також можна
скористатися формулою знаходження продуктивності. У цьому випадку рішення
приймає такий вигляд:
Ппершого пекаря = А : t = 40 : 10 = 4 бул./хв.
Пдругого пекаря = А : t = 15 : 5 = 3 бул./хв.
ЗАДАЧА:
Принтер
надрукував 350 сторінок за 5
годин. З якою продуктивністю він працював ?
РОЗВ'ЯЗАННЯ:
Якщо
протягом 5 годин принтер надрукував 350
сторінок, то протягом години він надрукував 350 : 5. Тобто працював з продуктивністю 70
сторінок на годину:
350
: 5 = 70 стор./год.
Також,
рішення можна записати за допомогою формули знаходження продуктивності:
П = А : t = 350 : 5 = 70 стор./час.
ЗАДАЧА:
Тато виконує
всю роботу за 4 години, а його син – за 7 годину. Яку частину роботи вони зроблять разом за 1 годину ?
РОЗВ'ЯЗАННЯ:
Нехай вся
робота дорівнює 1. Тоді продуктивність тата:
1 : 4 = 1/4,
а
продуктивність сина:
1 : 7 = 1/7.
Продуктивність
загальна:
1/4 + 1/7 = 7/28 + 4/28 = 11/28.
Іноді слово <<продуктивність>> може бути замінена на слово
<<швидкість>>, <<ефективність>>,
<<продуктивність>>, <<плідність>>.
ЗАДАЧА:
Петру треба за
2 дні прочитати книгу, в якій 100 сторінок.
Першого дня він читав 4 години зі швидкістю 12 сторінок на годину. З якою швидкістю йому треба читати частину книги, що
залишилася, якщо в нього є на це 4 години ?
РОЗВ'ЯЗАННЯ:
Дізнаємось,
скільки сторінок Петя прочитав у перший день. Він читав 12 сторінок на годину. Читанню першого дня він присвятив 4 години, тому для знаходження кількості прочитаних сторінок у перший
день, потрібно 12 помножити на 4.
12 ∙ 4 = 48 сторінок прочитав першого дня.
Дізнаємось,
скільки сторінок залишилося почитати. Віднімемо із загальної кількості сторінок
(100)
кількість прочитаних сторінок (48).
100 – 48 = 52 (стор.).
Залишилось
прочитати 52 сторінки.
Тепер знайдемо таку продуктивність, коли Петя зможе прочитати 52 сторінки за 4 години. Розкидаємо 52 сторінки на 4
години порівну:
52 : 4 = 13 сторінок на годину.
Якщо відомі
продуктивність та час роботи, то можна знайти виконану роботу.
Виконана робота
дорівнює продуктивності помноженої на час роботи.
Формула для роботи:
А
= П∙ t.
ЗАДАЧА:
Якщо продуктивність пекаря становить 50 булочок на годину, і він пропрацював 4 години, то можна знайти всю виконану роботу за ці чотири години. Для цього
продуктивність (50 бул./год) потрібно помножити на час його роботи (4 год):
50 ∙ 4 = 200 булочок.
ЗАДАЧА:
Принтер
працює з продуктивністю 70 стор/год. Скільки сторінок він
надрукує за 5 годин
?
РОЗВ'ЯЗАННЯ:
Якщо
за годину принтер друкує 70 сторінок, то за 5
годин він надрукує в 5 разів більше:
70
∙ 5 = 350 сторінок.
Також
рішення можна записати за допомогою формули знаходження роботи. У цьому випадку
кількість надрукованих сторінок є виконаною роботою:
А = П ∙ t = 70 ∙ 5 = 350 сторінок.
ЗАДАЧА:
Через
першу трубу басейн можна заповнити за 20 годин, а через другу за 30
годин. Яка частина басейну заповниться через обидві труби за 1
годину ?
РОЗВ'ЯЗАННЯ:
Робота
у разі це заповнення басейну. Позначимо цю роботу через одиницю:
А = 1.
Продуктивність заповнення басейну через першу трубу виражатиметься дробом 1/20, через другу трубу – дробом 1/30. Спільна продуктивність висловлюватиметься дробом 1/12.
Продуктивність визначення є робота, виконана за одиницю часу. Отже, дріб 1/12 є відповіддю завдання, оскільки нас цікавило, яка частина басейну заповниться через обидві труби за годину. Це можна перевірити, скориставшись формулою знаходження роботи. Змінна П у нас має значення 1/12, а змінна t дорівнює одиниці (однієї години). Формула знаходження роботи дозволить нам визначити, яка частина роботи буде виконана за одну годину:ЗАДАЧА:На
прокладку траншеї потрібно витратити 10 год. Екскаватор пропрацював 8
годин, після чого йому залишилося пройти 50
м. Знайдіть загальну довжину траншеї.
РОЗВ'ЯЗАННЯ:
У
задачі мається на увазі, що екскаватор працював з однаковою продуктивністю
протягом усієї роботи. На роботу потрібно витратити 10
год. Опрацьовано було 8 год. Отже, залишилося ще 2 год. На 2 години припадає 50 м
траншеї, що залишилися. Якщо поділити 50 м на 2,
то можна визначити, скільки метрів екскаватор прокладає за одну годину.
50 : 2 = 25 м/год.
За
годину екскаватор прокладав 25 м. Працював він 10
год. Помножимо 25 на 10, ми визначимо загальну довжину
траншеї.
25 ∙ 10 = 250 м.
Якщо відомі робота та
продуктивність, то можна знайти час роботи.
Час
роботи дорівнює відношенню виконаної роботи до продуктивності.
Формула для знаходження часу:
t = А : П.
ЗАДАЧА:
Якщо
на тиждень бригада відбудовує 2 поверхи, то можна дізнатися,
скільки тижнів знадобиться для відбудови 8
поверхів. Щоб визначити час відбудови восьми поверхів, потрібно виконану роботу
(8 поверхів) поділити на продуктивність (2 поверх/тиж.).
8
: 2 = 4 тиж.
Якщо
за тиждень будуються 2 поверхи, то 8 поверхів
буде відбудовано за чотири тижні. У цьому випадку вся робота дорівнювала
восьми. Продуктивність дорівнювала двом, оскільки за визначенням продуктивність
є робота, виконана за одиницю часу – у нашому випадку два поверхи за тиждень.
ЗАДАЧА:
Принтер
працював із продуктивністю 70 сторінок на годину та надрукував 350
сторінок. Визначте час роботи принтера.
РОЗВ'ЯЗАННЯ:
Вираз
«принтер працював з продуктивністю 70 сторінок на годину» означає, що в
кожній годині принтер друкував по 70 сторінок. І це тривало доти, доки
він не надрукував 350 сторінок. Очевидно, що розділивши 350
сторінок по 70, ми визначимо час роботи принтера,
тобто дізнаємось скільки годин він працював.
350
: 70 = 5 год.
Також
рішення можна записати за допомогою формули знаходження часу:
t
= А : П = 350 :
70 = 5 год
ЗАДАЧА:
Якщо 12 робочих виконують певну роботу за 3 дні, то за скільки днів цю роботу
виконають 4 робочих, працюючи з однаковою
продуктивністю ?
РОЗВ'ЯЗАННЯ:
Оскільки
завдання говориться про роботу 12 людина, це
завдання спільну роботу. Так як обсяг роботи не відомий, то приймемо його за 1.
Нехай їх
частин роботи на день – це продуктивність 1 робітника. Спільна робота дорівнює сумі продуктивністю кожного з
робітників. Оскільки робочих 12 і вони однакова продуктивність, то:
П12
= 12П1 = 12х.
Скористаємося
формулою спільної продуктивності, згідно з якою:
П = А : t.
Так як 12 робітників виконають роботу за 3 дні, то:
t12
= 3 дні.
Підставимо всі значення у формулу:
12х = 1/3
Знайдемо х:
х = 1/36 – частин роботи на
день.
Отже, продуктивність 1-го робітника 1/36 частин роботи на день. Знайдемо
час виконання роботи, коли працює 4 робітника. Скористаємося формулою часу:
t4
= А : П4.
Знайдемо продуктивність 4-х робітників:
П4
= 4П1 = 4х = 4 ∙ 1/36 =
1/9.
Тоді:
t4
= А : П4 = 1 : 1/9 = 9 (днів).
ЗАДАЧА:
Одна труба
може заповнити басейн за чотири години. Друга – за шість годин. За який час
заповниться басейн, якщо обидві труби увімкнути одночасно ?
РОЗВ'ЯЗАННЯ:
Так як труби
працюють разом, складають їхню продуктивність.
Для першої
труби, яка заповнює басейн за 4 години:
П = А : t = 1 : 4 = 1/4 – за годину заповнить перша труба.
Для другої
труби, яка заповнює басейн за 6 год:
П = А : t = 1 : 6 = 1/6 – за годину заповнить друга труба.
Разом, при
спільній роботі, труби заповнять за годину:
1/4 + 1/6 = 3/12 + 2/12 = 5/12 – дві труби за годину.
Обсяг роботи –
1 басейн. Спільна продуктивність 5/12 басейну за годину. Тоді час
заповнення басейну буде:
t
= А : П = 1 : 5/12
= 1 ∙ 12/5 = 12/5 (год).
ЗАДАЧА:
Кінь з'їдає копицю сіна за 1 добу, корова
може з'їсти таку ж копицю за 3 доби, а вівця за 6 діб. За який
час з'їдять цю копицю коня, корова та вівця разом ?
РОЗВ'ЯЗАННЯ:
Робота в даному випадку це з'їдання копиці сіна.
Позначимо її через одиницю:
А = 1.
Посудина
наповнюється шлангом за 12 хв, а повна
посудина спорожняється при відкритті крана за 20 хв. За який час наповниться порожня посудина, якщо одночасно відкрити
кран і вливати воду через шланг ?
РОЗВ'ЯЗАННЯ:
Робота у разі
це наповнення судини. Позначимо цю роботу через одиницю:
А = 1.
Визначимо час, за який наповниться порожня посудина, якщо одночасно відкрити кран і вливати в нього воду через шланг,Завдання до уроку 23
- Урок 1. Відношення величин
- Урок 2. Пропорції
- Урок 3. Величини прямо пропорціональні
- Урок 4. Величини обернено пропорціональні
- Урок 5. Пропорціональний поділ
- Урок 6. Відсотки
- Урок 7. Знаходження процентів даного числа (задачі)
- Урок 8. Знаходження числа за його процентами (задачі)
- Урок 9. Знаходження процентного відношення двох чисел
- Урок 10. Прості та складні відсотки
- Урок 11. Задачі на час
- Урок 12. Задачі на знаходження двох чисел за їх сумою і різницею
- Урок 13. Задачі на знаходження двох чисел за їх сумою або різницею і відношенням
- Урок 14. Середнє арифметичне
- Урок 15. Середнє арифметичне (задачі)
- Урок 16. Масштаб на планах та картах
- Урок 17. Визначення відстані на місцевості
- Урок 18. Визначення відстані на карти або плані
- Урок 19. Задачі на зустрічний рух
- Урок 20. Задачі на рух в одному напрямі
- Урок 21. Задачі на рух у протилежних напрямках
- Урок 22. Задачі на рух по воді





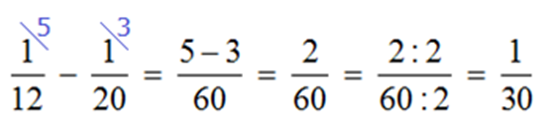

Комментариев нет:
Отправить комментарий