ВІДЕОУРОК
Швидкість і час за однакової довжини шляху. Якщо
швидкість зменшується, час збільшується, і якщо швидкість збільшується, той час
зменшується.
Кількість робітників та час при
визначенні обсягу робіт. За
виконання однієї й тієї роботи, що менше працівників, тим більше потрібно часу,
щоб виконати цю роботу і навпаки.
Якщо
12
робітників виконують певну роботу за 3 дні, то за скільки днів цю ж
роботу виконають 4 робітники, працюючи з однаковою
продуктивністю ?
РОЗВ'ЯЗАННЯ:
Тривалість
роботи певного числа робітників і кількість робітників при однаковій
продуктивності праці кожного робочого величини обернено пропорційні.
Чим
більше робітників працює, тим менше часу знадобиться, щоб виконати роботу.
Чим
менше робочих працює, тим більше часу знадобиться, щоб виконати роботу.
За
визначенням пропорційних величин їх добуток постійний. Тоді знайдемо їхні
добутки та прирівняємо їх.
Перша
пара обернено пропорційних величин:
12
робітників виконують роботу за 3 дні.
Друга
пара обернено пропорційних величин:
4
робітники виконують роботу за х днів.
Можемо
записати:
12
∙ 3 = 4 ∙
х.
ВІДПОВІДЬ: 9
днів
ЗАДАЧА:
Бригада
робітників із 5 осіб може пофарбувати приміщення
за 6
днів. Скільки днів потрібно на виконання цієї роботи бригаді з 3
осіб
?
РОЗВ'ЯЗАННЯ:
Тривалість
роботи певного числа робітників і кількість робітників при однаковій
продуктивності праці кожного робочого величини обернено пропорційні.
Чим
більше робітників працює, тим менше часу знадобиться, щоб виконати роботу.
Чим
менше робочих працює, тим більше часу знадобиться, щоб виконати роботу.
За
визначенням пропорційних величин їх добуток постійний. Тоді знайдемо їхні добутки
та прирівняємо їх.
Перша
пара обернено пропорційних величин:
5
осіб фарбують приміщення за 6 днів.
Друга
пара обернено пропорційних величин:
3
людей фарбують приміщення за х днів.
Можемо
записати:
5
∙ 6 = 3 ∙
х.
ВІДПОВІДЬ: 10
днів
ЗАДАЧА:
4
сівалки можуть засіяти поле за 18 днів. За який час буде засіяно це
поле, якщо працюватимуть три сівалки з тією ж продуктивністю ?
РОЗВ'ЯЗАННЯ:
Тривалість
роботи певного числа сівалок та число сівалок при однаковій продуктивності
кожної сівалки, величини обернено пропорційні.
Чим
більше сівалок працює, тим менше часу потрібно, щоб засіяти поле.
Чим
менше сівалок працює, тим більше часу знадобиться, щоб засіяти поле.
За
визначенням пропорційних величин їх добуток постійний. Тоді знайдемо їхні добутки
та прирівняємо їх.
Перша
пара обернено пропорційних величин:
4
сівалки засіюють поле за 18 днів.
Друга
пара обернено пропорційних величин:
3
сівалки засіюють поле за х днів.
Можемо
записати:
4
∙ 18 = 3 ∙
х.
ВІДПОВІДЬ: 24
дні
ЗАДАЧА:
Засипати
котлован 3
бульдозери можуть за 20 днів. За скільки днів виконають цю
роботу 5
бульдозерів ?
РОЗВ'ЯЗАННЯ:
Тривалість
роботи певного числа бульдозерів та кількість бульдозерів при однаковій
продуктивності кожного бульдозера, величини обернено пропорційні.
Чим
більше бульдозерів працює, тим менше часу знадобиться, щоб засипати котлован.
Чим
менше бульдозерів працює, тим більше часу знадобиться, щоб засипати котлован.
За
визначенням пропорційних величин їх добуток постійний. Тоді знайдемо їхні добутки
та прирівняємо їх.
Перша
пара обернено пропорційних величин:
3
бульдозери засипають котлован за 20 днів.
Друга
пара обернено пропорційних величин:
5
бульдозерів засипають котлован за 10 днів.
Можемо
записати:
3
∙ 20 = 5 ∙
х.
ВІДПОВІДЬ: 12
днів
ЗАДАЧА:
4
однакові труби заповнюють басейн водою за 56
хвилин. За скільки хвилин можна заповнити басейн водою за допомогою 7
таких труб ?
РОЗВ'ЯЗАННЯ:
Так
як чим більше буде труб, тим менше часу знадобиться для заповнення басейну
водою, то час заповнення басейну обернено пропорційно кількості труб.
За
визначенням пропорційних величин їх добуток постійний. Тоді знайдемо їхні добутки
та прирівняємо їх.
Перша
пара обернено пропорційних величин:
4
однакові труби заповнюють басейн водою за 56
хвилин.
Друга
пара обернено пропорційних величин:
7
однакових труб заповнюють басейн водою за х
хвилин.
Можемо
записати:
4
∙ 56 = 7 ∙
х.
ЗАДАЧА:
Звідси:
Плата за проїзд залізницею зростає залежно від відстані: чим далі ми їдемо, тим більше платимо, але це не значить, що плата пропорціональна відстані.
- Урок 1. Відношення величин
- Урок 2. Пропорції
- Урок 3. Величини прямо пропорціональні
- Урок 5. Пропорціональний поділ
- Урок 6. Відсотки
- Урок 7. Знаходження процентів даного числа (задачі)
- Урок 8. Знаходження числа за його процентами (задачі)
- Урок 9. Знаходження процентного відношення двох чисел
- Урок 10. Прості та складні відсотки
- Урок 11. Задачі на час
- Урок 12. Задачі на знаходження двох чисел за їх сумою і різницею
- Урок 13. Задачі на знаходження двох чисел за їх сумою або різницею і відношенням
- Урок 14. Середнє арифметичне
- Урок 15. Середнє арифметичне (задачі)
- Урок 16. Масштаб на планах та картах
- Урок 17. Визначення відстані на місцевості
- Урок 18. Визначення відстані на карти або плані
- Урок 19. Задачі на зустрічний рух
- Урок 20. Задачі на рух в одному напрямі
- Урок 21. Задачі на рух у протилежних напрямках
- Урок 22. Задачі на рух по воді
- Урок 23. Задачі на спільну роботу





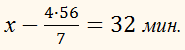





Комментариев нет:
Отправить комментарий