ВИДЕО УРОК
При нерівномірному русі миттєва швидкість тіла безперервно змінюється: від точки до точки, від одного моменту часу до іншого. Як же вичислити швидкість у будь-який момент часу ? Для цього треба знати, як швидко змінюється швидкість, або, іншими словами, яка її зміна в її зміну в одиницю часу. Для простоти ми розглядатимемо такий нерівномірний рух тіла, при якому його швидкість за будь-які рівні проміжки часу змінюється однаково. Такий рух називається рівноприскореним.
Рух, при якому швидкість за будь-які рівні проміжки часу змінюється однаково, називають рівноприскореним рухом.
Прискорення.
Якщо в деякий початковий момент часу швидкість тіла рівна
а через проміжок часу t вона виявляється рівною
те за кожну одиницю часу швидкість змінюється на
Величина
характеризує швидкість виміру швидкості. Її називають прискоренням і означають буквою а:
Якщо прискорення тіла по абсолютному значенню велике, то це означає, що воно швидко набирає швидкість (коли тіло розгониться) або швидко втрачає його (при гальмуванні).
те за кожну одиницю часу швидкість змінюється на
Величина
характеризує швидкість виміру швидкості. Її називають прискоренням і означають буквою а:
Прискоренням
тіла, що рухається, називають величину, рівну відношенню зміни швидкості тіла
до проміжку часу, в течії якого ця зміна сталася.
Якщо прискорення тіла по абсолютному значенню велике, то це означає, що воно швидко набирає швидкість (коли тіло розгониться) або швидко втрачає його (при гальмуванні).
відомо, то можна вичислити значення швидкості
тіла у будь-який момент часу, якщо відоме ще і значення початкової швидкості
З формули
витікає, що
Прискорення і треба знати для обчислення швидкості
Оскільки прискорення дорівнює добутку векторної величини
на скаляр
тіла у будь-який момент часу, якщо відоме ще і значення початкової швидкості
З формули
витікає, що
Прискорення і треба знати для обчислення швидкості
Оскільки прискорення дорівнює добутку векторної величини
на скаляр
воно саме є векторною
величиною.
У яких одиницях
вимірюють прискорення ?
Оскільки
те абсолютне значення
прискорення дорівнює одиниці, якщо дорівнює одиниці абсолютне значення зміни
швидкості і дорівнює одиниці проміжок часу.
Поклавши у формулі
прискорення
v – v0 = 1 м/сек і
t = 1 сек,
отримаємо одиницю прискорення в системі СІ:
т. е. за одиницю
прискорення в системі СІ
приймається прискорення такого рівнозмінного руху, при якому за кожну
секунду швидкість змінюється на 1 м/сек. Найменування одиниці
прискорення читається так: <<метр в секунду за секунду>>, або
<<метр, що ділиться на секунду в квадраті>>. У системі СГС за
одиницю прискорення приймають 1 cм/сек2.
За одиницю прискорення приймають прискорення такого руху, при якому за одиницю часу швидкість змінюється на одиницю швидкості.
Напрям прискорення.
При прямолінійному русі вектори
спрямовані уздовж однієї прямої, яка являється в
той же час і траєкторією руху. Уздовж цієї ж прямої у напрямі руху тіла ми
умовилися направляти і координатну вісь (вісь Х). У такому разі вектор
різниці
а значить і вектор прискорення
а значить і вектор прискорення
лежить на тій же
прямій. Але куди він спрямований – у бік руху (так само як вісь Х) або проти нього ?
Проекція
різниці двох векторів на яку-небудь вісь дорівнює різниці з проекцій на ту ж
вісь. Отже, для проекцій векторів
на вісь Х можна написати
Тут а – проекція вектору
на вісь Х; v і v0 – проекція векторів
ПЕРШИЙ ВИПАДОК
Швидкість тіла по абсолютному значенню росте (тіло << розгониться >>). Це означає, що v ˃ v0. Тоді з формули
Тут а – проекція вектору
на вісь Х; v і v0 – проекція векторів
на тугіше вісь.
Оскільки усі три
вектори лежать на одній прямій (осі Х),
то абсолютні значення їх проекцій дорівнюють абсолютним значенням самих
векторів.
Розглянемо 2
випадки прискореного руху тіла.
ПЕРШИЙ ВИПАДОК
Швидкість тіла по абсолютному значенню росте (тіло << розгониться >>). Це означає, що v ˃ v0. Тоді з формули
видно, що проекція прискорення а
позитивна і рівна
Вектор
ПРИКЛАД:
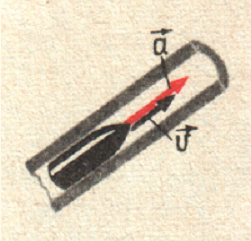
Коли бронебійний снаряд рухається при пострілі в стволі гармати, його швидкість росте і прискорення спрямоване так само як і швидкість.
Вектор
Отже, спрямований так
само, як вісь Х,
т. е. у бік руху.
ПРИКЛАД:
Коли бронебійний снаряд рухається при пострілі в стволі гармати, його швидкість росте і прискорення спрямоване так само як і швидкість.
З формули
видно, що проекція прискорення
в цьому випадку, негативна:
З формули
можна отримати вираження для швидкості v:
v = v0 + at.
видно, що проекція прискорення
в цьому випадку, негативна:
З формули
можна отримати вираження для швидкості v:
v = v0 + at.
У цій формулі
v, v0 и a – проекції векторів
на вісь Х,
які можуть бути як позитивними, так і негативними.
При
рішенні завдань вираження для швидкостіv = v0 + at
зручно записати так,
щоб з нього відразу було видно, як спрямований вектор прискорення.
Якщо
швидкість тіла росте (розгін), то
Коли ж швидкість тіла зменшується (гальмування),
Зрозуміло, що тіло, яке гальмується, повинне колись зупинитися. Це станеться, як це видно з формули
тоді, коли
стане рівним v0, тобто у момент часу
Але якщо прискорення залишається постійним (по модулю і напряму) і після цього моменту, то тіло, зупинившись, почне рухатися в протилежну сторону. Це видно з того, що при
величина
Зрозуміло, що тіло, яке гальмується, повинне колись зупинитися. Це станеться, як це видно з формули
тоді, коли
стане рівним v0, тобто у момент часу
Але якщо прискорення залишається постійним (по модулю і напряму) і після цього моменту, то тіло, зупинившись, почне рухатися в протилежну сторону. Це видно з того, що при
величина
стане більше, ніж v0;
швидкість v змінить свій знак на зворотний. Так рухається
тіло, кинуте вертикально вгору: долетівши до вищої точки траєкторії, тіло
починає рух вниз.
Якщо v0 = 0 і вектор прискорення спрямований
також, як і вісь координат, то з формули
витікає, що
Якщо ж вісь координат вибрана так, що напрям вектору прискорення протилежний до напряму осі координат, то з формули
витікає, що
У усіх системах відліку, що рухаються один відносно одного прямолінійно і рівномірно, прискорення тіла однакове.
Але прискорення тіла будуть різними в системах відліку, що рухаються з прискоренням один відносно одного. В цьому випадку прискорення складаються так само як швидкості.
ЗАДАЧА:
Автомобіль проїжджає повз спостерігача, рухаючись із швидкістю 10 м/сек. У цей момент водій натискає на гальмо, і автомобіль починає рухатися з прискоренням 1 м/сек2. Скільки часу пройде з того моменту, коли водій натиснув на гальмо, до зупинки автомобіля ?
РОЗВ'ЯЗАННЯ:
Виберемо за початок відліку те місце, в якому знаходиться спостерігач, і направимо координатну вісь у бік руху автомобіля. Тоді проекція швидкості автомобіля на цю вісь буде позитивною. Оскільки швидкість автомобіля зменшується, то проекція прискорення негативна і ми повинні скористатися формулою:
Якщо ж вісь координат вибрана так, що напрям вектору прискорення протилежний до напряму осі координат, то з формули
витікає, що
Знак <<–>> в цій формулі означає,
що вектор швидкості, так само як і вектор прискорення, спрямований протилежно
напряму осі координат. Модуль швидкості, звичайно, і в цьому випадку
збільшується з часом.
Зазвичай називають рух
зі швидкістю, що зростає за абсолютною величиною, прискореним рухом, а рух з убуваю
чиї швидкістю – уповільненим рухом. Але в механіці будь-який нерівномірний рух
є прискореним рухом. Чи рушає автомобіль з місця або гальмує, в обох випадках
він рухається з прискоренням. Прискорений прямолінійний рух відрізняється від
уповільненого тільки знаком проекції вектору прискорення.
Переміщення, швидкість
і траєкторія руху різні відносно різних тіл відліку, що рухаються один відносно
одного.
А прискорення ? Чи
відносно воно ?
Прискорення тіла
визначається векторною різницею двох значень його швидкості в різні моменти
часу. При переході від однієї системи координат до іншої, що рухається відносно
першою рівномірно і прямолінійно, зміняться обидва значення швидкості. Але
змінюються вони на одну і ту ж величину. Різниця ж їх залишиться незмінною.
Тому і прискорення залишиться незмінним.
У усіх системах відліку, що рухаються один відносно одного прямолінійно і рівномірно, прискорення тіла однакове.
Але прискорення тіла будуть різними в системах відліку, що рухаються з прискоренням один відносно одного. В цьому випадку прискорення складаються так само як швидкості.
ЗАДАЧА:
Автомобіль проїжджає повз спостерігача, рухаючись із швидкістю 10 м/сек. У цей момент водій натискає на гальмо, і автомобіль починає рухатися з прискоренням 1 м/сек2. Скільки часу пройде з того моменту, коли водій натиснув на гальмо, до зупинки автомобіля ?
РОЗВ'ЯЗАННЯ:
Виберемо за початок відліку те місце, в якому знаходиться спостерігач, і направимо координатну вісь у бік руху автомобіля. Тоді проекція швидкості автомобіля на цю вісь буде позитивною. Оскільки швидкість автомобіля зменшується, то проекція прискорення негативна і ми повинні скористатися формулою:
Звідси
Підставляючи в цю формулу чисельні значення заданих величин, отримаємо:
За позитивний напрям координатної осі можна прийняти і напрям, протилежний до руху. Тоді проекція початкової швидкості автомобіля буде негативною (v0 = –10 м/сек), а проекція прискорення – позитивною, і застосовувати тоді треба формулу:
Звідси
Вимір прискорення.
Підставляючи в цю формулу чисельні значення заданих величин, отримаємо:
За позитивний напрям координатної осі можна прийняти і напрям, протилежний до руху. Тоді проекція початкової швидкості автомобіля буде негативною (v0 = –10 м/сек), а проекція прискорення – позитивною, і застосовувати тоді треба формулу:
Звідси
Результат
вийшов той же.
Вимір прискорення.
Простий спосіб виміру прискорення полягає в наступному. На тіло, що рухається рівно прискорено, поміщають крапельницю, т. е. посудина із забарвленою рідиною, з якої через певні рівні проміжки часу витікають краплі.
Краплі, що падають,
вказують положення тіла через однакові і відомі проміжки часу, які ми позначимо
буквою τ. Різниця відстаней між
краплями, що впали, за два будь-яких наступних один за одним проміжку часу τ
рівна aτ2, де а – прискорення. Вимірявши довжини l1 і l2 двох сусідніх проміжків між краплями, ми і
знайдемо прискорення по формулі
l2 – l1 = aτ2,
звідки
Часто користуються іншим, точнішим способом. Це
так званий стробоскопічний метод. Він
полягає в тому, що тіло, що рухається, в темряві освітлюють через рівні
проміжки часу світловим спалахом. Ясно, що тіло буде видне тільки в тих
положеннях, в яких воно виявляється освітленим. Якщо тіло в процесі його руху
фотографувати (затвор фотоапарата має бути відкритий в плині усього часу руху),
то на фотографічній плівці будуть видні послідовні положення тіла через рівні
проміжки часу. Вимірюючи відстані між зображеннями тіла на плівці і знаючи
проміжки часу між світловими спалахами, можна вичислити прискорення, якщо
відомий масштаб зображення. Малюнок
є копією з фотографії
кулі, що падає, отриманої методом спалахів. Поруч поміщена шкала для виміру
відстані.
Слід
зауважити, що вивчення прямолінійного рівноприскореного руху дещо скрутне через
те, що тіло, що рухається, досить швидко зникає від спостерігача. Так,
наприклад, для кульки, на фотографії
проміжки часу між спалахами складали всього
біля 0,03 сек, так
що рух тривав усього біля 0,5 сек.
- Урок 1. Рух матеріальної точки
- Урок 2. Рівномірний прямолінійний рух
- Урок 3. Графік швидкості і шляху рівномірного прямолінійного руху
- Урок 4. Векторні і скалярні величини
- Урок 5. Дії над векторами
- Урок 6. Нерівномірний прямолінійний рух
- Урок 8. Переміщення при прямолінійному рівноприскореному русі
- Урок 9. Середня швидкість при прямолінійному рівноприскореному русі. Зв'язок між переміщенням і швидкістю.
- Урок 10. Приклади прямолінійного рівноприскореного руху
- Урок 11. Криволінійний рух
- Урок 12. Рух по колу
- Урок 13. Обертання твердого тіла



















































Комментариев нет:
Отправить комментарий