ВИДЕО УРОК
Определение производной базируется на понятии
предела.
Понятие возрастания, убывания, максимума, минимума функции.
Представьте, что нам предстоит путешествие в город, до которого можно добраться разными путями. Сразу откинем кривые петляющие дорожки, и будем рассматривать только прямые магистрали. Однако прямолинейные направления тоже бывают разными. До города можно добраться по ровному автобану. Или по холмистому шоссе – вверх-вниз, вверх-вниз. Другая дорога идёт только в гору, а ещё одна – всё время под уклон. Экстремалы выберут маршрут через ущелье с крутым обрывом и отвесным подъёмом.
Но каковы бы ни были предпочтения, желательно
знать местность или, по меньшей мере, располагать её топографической картой. А
если такая информация отсутствует ? Ведь можно выбрать, например, ровный путь,
да в результате наткнуться на горнолыжный спуск. Не факт, что навигатор и даже
спутниковый снимок дадут достоверные данные. Поэтому неплохо бы формализовать
рельеф пути средствами математики.
Рассмотрим некоторую дорогу
y = f(x)
(вид сбоку)
Какие особенности у данного графика ?
На интервалах
(–∞; a), (b, +∞)
функция возрастает, то есть каждое следующее
её значение больше предыдущего. График идёт снизу вверх (забираемся на горку).
А на интервале
(a,b)
функция убывает – каждое следующее значение
меньше предыдущего, и график идёт сверху вниз (спускаемся по склону).
Также обратите внимание на особые точки. В
точке х = а мы достигаем максимума, то есть существует такой участок пути, на котором
значение f(а)
будет самым большим (высоким). В точке же х = b достигается
минимум, и существует такая её окрестность, в которой значение f(b) самое маленькое (низкое).
На промежутках
(–∞; a), (b, +∞)
функция возрастает, но возрастает она с
разной скоростью. И первое, что бросается в глаза, – на интервале (–∞; a)
график взмывает вверх гораздо более круто, чем на интервале (b, +∞). Нельзя ли измерить крутизну дороги с помощью математического
инструментария ?
Скорость изменения функции.
Идея состоит в следующем:
Рассмотрим полученную дробь.
Пусть изначально мы находимся на
высоте 29 метров (в левой чёрной иочке). Преодолев
расстояние ∆х = 10 метров (левая красная линия), мы
окажемся на высоте 60 метров. Тогда
приращение функции составит
∆у1 = 60 – 20 = 40 (м)
(зелёная линия) и:
2) Теперь пройдём то же самое расстояние ∆х от самой правой чёрной точки. Здесь подъём более пологий, поэтому приращение ∆у3 (малиновая линия) относительно невелико, и отношение
Условно говоря,
∆х = 10 м, ∆у3 = 5 м
и скорость роста функции составляет
то есть, здесь на каждый метр пути
приходится в среднем пол метра подъёма.
3) Посмотрим на верхнюю чёрную точку, расположенную на оси ординат. Предположим, что это отметка 50 м. Снова преодолеваем расстояние ∆х = 10 м, в результате чего оказываемся ниже – на уровне 30 м. Поскольку осуществлено движение сверху вниз, то итоговое приращение функции (высоты) будет отрицательным:
∆у2 = 30 – 50 = –20 (м)
∆х = 10 м, ∆у3 = 5 м
и скорость роста функции составляет
3) Посмотрим на верхнюю чёрную точку, расположенную на оси ординат. Предположим, что это отметка 50 м. Снова преодолеваем расстояние ∆х = 10 м, в результате чего оказываемся ниже – на уровне 30 м. Поскольку осуществлено движение сверху вниз, то итоговое приращение функции (высоты) будет отрицательным:
∆у2 = 30 – 50 = –20 (м)
(коричневый отрезок на чертеже). И в данном случае речь идёт о скорости убывания функции:
Какое значение <<измерительного эталона>> ∆х лучше всего использовать ? Совершенно понятно, 10 м – это весьма грубо. На них запросто уместится добрая дюжина кочек. Таким образом, при десятиметровом мы не получим вразумительной характеристики подобных участков пути посредством отношения
Более того, справедливы следующие факты:
– для любой точки подъёмов
(–∞; a), (b, +∞)
можно подобрать значение ∆х (пусть и
очень малое), которое умещается в границах того или иного подъёма. А это
значит, что соответствующее приращение высоты
∆у будет
гарантировано положительным, и неравенство
Аналогично, для любой точки склона (a, b) существует значение ∆х, которое полностью уместится на этом склоне. Следовательно, соответствующее приращение высоты ∆у однозначно отрицательно, и неравенство
Особо интересен случай, когда скорость изменения функции равна нулю:
Производная функция в точке.
Рассмотрим функцию y = f(x) (синий график), которая определена и непрерывна на некотором интервале, произвольную точку х0, принадлежащую данному интервалу, и соответствующее значение f(x).
f(х0 + ∆х).
приращение аргумента ∆х повлекло за собой приращение функции
∆у = f(х0 + ∆х) – f(х0)
(малиновый отрезок).
В данном случае ∆у ˃ 0, поскольку в качестве примера выбран промежуток, на
котором функция возрастает.
На рисунке проведена секущая KL (коричневая прямая) и прямоугольный
треугольник KLN. угол наклона секущей к оси ОХ
обозначен через α и
отмечен коричневой дугой в двух местах. Этот угол однозначно определяется
приращениями ∆х и ∆y. Рассмотрим прямоугольный треугольник KLN и угол α = ∠ LKN. Тангенс этого угла равен отношению
противолежащего катета к прилежащему катету:
Геометрический
смысл производной.
Если взять линейку и совместить её ребро с прямой LN, и, согласно определению производной
медленно двигать линейку влево к точке х0, уменьшая тем самым приращение ∆х, то мы увидим, что приращение функции
∆y = LN тоже
уменьшается: точка N будеь бесконечно близко приближаться к
точке K по горизонтали (красному отрезку),
и точка L – бесконечно близко приближаться к той же точке К, но уже по графику функции y = f(x) (синей линии).
Касательная к графику функции в точке – это предельное положение секущей в данной точке.
Рассмотрим формулу тангенса угла наклона секущей
и осуществим в обеих её частях, так
называемый предельный переход.
При бесконечном уменьшении ∆х и
нахождения предела
угол наклона
α секущей KL стремится к углу
наклона φ касательной
В итоге:
Производная функции в точке х0 численно равна тангенсу угла наклона
касательной к графику функции в данной точке:
Тангенс угла наклона касательной – это её
угловой коэффициент:
ПРИМЕР:
Для касательной
Он показывает, как и правосторонний предел,
рост функции в точке x0.
Понятие производной функции.
Возьмём формулу производной в точке
и заменим в ней
x0 на х:
Для функции
y = f(x) по закону
ставится в соответствии другая функция у' = f
' (x), которая называется производной
функцией (или просто производной).
1) Если f ' (x0) ˃ 0, то функция y = f(x) возрастает в точке x0. И, очевидно существует интервал (пусть даже очень малый), содержащий точку x0, на котором функция y = f(x) растёт, и её график идёт <<снизу вверх>>.
2) Если f ' (x0) < 0, то функция y = f(x) убывает в точке x0. И существует интервал, содержащий точку x0, на котором функция
3) Если f ' (x0) = 0, то бесконечно близко около точки x0 функция
Термины, истолковывающие механический смысл производной.
Рассмотрим закон изменения координаты тела x(t), зависящей от времени t, и функцию скорости движения данного тела v(t). Функция v(t) характеризует скорость изменения координаты тела, поэтому является первой производеной функции x(t) по времени:
Если бы в природе не существовало понятие <<движение
тела>>, то не существовало бы и производного понятия <<скорость тела>>.
Ускорение тела а(t) – это скорость изменения скорости, поэтому:
Если бы в природе не существовало исходных понятий
<<движение тела>> и <<скорость движения тела>>, то не существовало бы и производного понятия
<<ускорение тела>>
Это <<ровная
дорога>>, то есть функция и не
возрастает и не убывает в каждой точке. Ни вверх и не вниз.
Тут нет
неопределённости:
ноль, делённый на бесконечно малое число
∆х, равен нулю.
Поскольку в качестве точки x0 можно взять любое <<икс>>, то проведём замену x0 = х и получим:
ПРИМЕР:
Поскольку в качестве
можно взять любое значение х, то
будет
неизменным.
ОТВЕТ: –2
Поскольку в качестве
x0 можно рассмотреть
любую точку х области
определнения функции
На интервале (–∞,
0) производная
отрицательна:
В результате секущая
KL стремится занять положение
касательной
y = kx + b
к графику функции
y = f(x)
в точке х0. Искомая касательная
изображена зелёным цветом.
Таким образом, мы получили строгое определение
касательной к графику функции.
Касательная к графику функции в точке – это предельное положение секущей в данной точке.
Рассмотрим формулу тангенса угла наклона секущей
y = kx + b
(последний дважды отмечен зелёными дугами).
Аналогичное утверждение справедливо и для тангенсов данных углов:
tg φ = k.
Для определения производной геометрическим
путём, необходимо:
– в точке определения производной провести
касательную;
– написать уравнение этой касательной, где
коэффициент при неизвестном и будет производной.
ПРИМЕР:
Для касательной
у = –х + 7/4,
производная
равна –1.
Для касательной
у = 2,
производная
равна 0.
Для касательной
у = 2х + 1,
производная
равна 2.
Для касательной
у = 4х – 2,
производная равна 4.
Рассмотрим уравнение прямой с угловым
коэффициентом:
Существование производной в точке и непрерывность функции.
По определению
следовательно, существование производной в
точке x0 тесно
связано с существованием предела
в данной точке.
y – y0 = k(x – x0).
Учитывая полученное равенство
f ' (x0) = tg φ = k,
перепишем уравнение в следующем виде:
y – y0 = f ' (x0)(x – x0).
Существование производной в точке и непрерывность функции.
По определению
В определении производной важнейшим является
тот факт, что приращение аргумента ∆х задаётся и в другую сторону.
Изобразите координатные оси, примерно такой
же график функции
y = f(x)
и точки x0, f(x0).
Отложите на чертеже небольшой отрезок ∆х слева
от точки x0. При этом точка
x0 + ∆х
расположится левее точки x0, а точка
f(x0 + ∆х)
– ниже точки f(x0). Теперь проведите
секущую графика функции
y = f(x)
и начните мысленно уменьшать
приращение ∆х вправо к точке x0. В результате данная секущая будет стремиться занять
положение той же самой <<зелёной>> касательной.
Приращение с левой стороны осуществляется <<против оси абсцисс>>
и поэтому отрицательно: ∆х < 0. Соответствующее приращение ∆у тоже меньше нуля, и поэтому
левосторонний предел будет положительным.
Правые и левые пределы конечны и совпадают,
что говорит о существовании общего предела, производной и единой касательной.
Таким образом, существование производной в
точке геометрически очень удобно ассоциировать с существованием общей касательной в данной точке.
Понятие производной функции.
Возьмём формулу производной в точке
Производная
у' = f
' (x)
характеризует скорость изменения функции
y = f(x).
y = f(x).
Рассмотрим некоторую точку x0 области
определения функции
y = f(x).
Функция непрерывна в данной точке. Тогда:
1) Если f ' (x0) ˃ 0, то функция y = f(x) возрастает в точке x0. И, очевидно существует интервал (пусть даже очень малый), содержащий точку x0, на котором функция y = f(x) растёт, и её график идёт <<снизу вверх>>.
2) Если f ' (x0) < 0, то функция y = f(x) убывает в точке x0. И существует интервал, содержащий точку x0, на котором функция
y = f(x)
убывает, и её график идёт <<сверху вниз>>.
3) Если f ' (x0) = 0, то бесконечно близко около точки x0 функция
y = f(x)
сохраняет свою скорость постоянной. Так
бывает у функции константы и в критических точках функции, в частности в точках
минимума и максимума.
Что понимается под словом <<производная>>
?
Функция
у' = f
' (x)
произошла от функции y = f(x).
Термины, истолковывающие механический смысл производной.
Рассмотрим закон изменения координаты тела x(t), зависящей от времени t, и функцию скорости движения данного тела v(t). Функция v(t) характеризует скорость изменения координаты тела, поэтому является первой производеной функции x(t) по времени:
Ускорение тела а(t) – это скорость изменения скорости, поэтому:
ПРИМЕР:
Используя
определение производной, доказать, что производная константы равна нулю.
РЕШЕНИЕ:
Функция константа
имеет вид
f(x) = С,
и графически – это
семейство прямых, параллельных оси абсцисс.
Изобразим график
функции
f(x) = 2.
Покажем
аналитически, что производная функции-константы равна нулю.
Рассмотрим
произвольное значение x0, в которм
f(x0) = С.
Придадим аргументу
приращение:
x0 + ∆х.
Функция всё время
постоянна, поэтому
f(x0+ ∆х) = С
и приращение
функции
∆у = f(x0+ ∆х) – f(x0) = С – С = 0.
По определению производной в точке:Поскольку в качестве точки x0 можно взять любое <<икс>>, то проведём замену x0 = х и получим:
Найти производную
функции:
f(x) = –2х
– 1.
по определению.
РЕШЕНИЕ:
Рассмотрим
произвольное значение x0, в котором
f(x0) = –2x0 – 1.
Зададим аргументу
приращение ∆х и вычислим соответствующее значение функции:
f(x0 + ∆х) = –2(x0 + ∆х) – 1 = –2x0 – 2∆х – 1.
Вычислим приращение функции:
∆у = f(x0 + ∆х) – f(x0)
=
–2x0 – 2∆х – 1 – (–2x0 – 1) =
–2x0 – 2∆х – 1 + 2x0 + 1 = –2∆х.
По определению производной в точке:
f '(x) = –2.
О чём говорит найденная
производная ?
Во-первых, для любого <<икс>>
она отрицательна, а значит, функция
f(x) = –2х
– 1
убывает на всей области определения.
Во-вторых, это убывание постоянно, то есть
<<наклон горки везде одинаков>> – в какой бы точке мы ни
находились, предельное отношение
Используя этот же алгоритм, можно решить
задачу в общем виде и доказать, что производная линейной функции
f(x) = kх + b
равна её угловому коэффициенту
f '(x) = k.
ПРИМЕР:
Найти производную функции
f(x) = х2
+ 2
по определению.
РЕШЕНИЕ:
Рассмотрим произвольную точку x0 и соответствующее
значение
f(x0) = (x0)2 + 2.
Зададим приращение
∆х и
вычислим значение функции в точке
x0 + ∆х.
f(x0 + ∆х) = (x0 + ∆х)2 + 2 =
(x0)2 + 2x0∆х + (∆х)2 + 2.
Найдём приращение функции:
∆у = f(x0 + ∆х) – f(x0)
=
(x0)2 + 2x0∆х + (∆х)2 + 2 – ((x0)2 + 2)
=
(x0)2 + 2x0∆х + (∆х)2 + 2 – (x0)2 – 2
=
2x0∆х + (∆х)2.
По определению производной в точке:
f(x) = х2
+ 2,
то проведём замену x0 = х
и получим
f '(x) = 2х.
Исходная функция
f(x) = х2
+ 2
и её производная
f '(x) = 2х.
– это
две совершенно разные функции, однако между ними существует чёткая и прзрачная
связь.
f '(x) < 0
(красная линия), что говорит об убывании функции f(x) на данном интервале. Ветвь параболы идёт сверху вниз.
А на интервале (0, +∞) производная
положительна:
f '(x) ˃ 0
(зелёная линия), значит, функция f(x) растёт на этом интервале, и её график идёт
снизу вверх.
При х = 0 производная равна
нулю:
f '(0) = 2 ∙ 0 = 0.
Найденное значение показывает, что скорость изменения
функции
f(x) = х2
+ 2
в точке х = 0 равна нулю (функция не растёт в ней и не убывает). В данном случае здесь минимум функции.
Всё это можно утверждать даже не зная, что такое парабола
и как выглядит график функции
f(x) = х2
+ 2.
Значение производной в точке выражает собой некоторую
меру скорости изменения функции в данной точке. Найдём несколько значений
производной.
f '(–0,5) = 2 ∙ (0,5) = –1,
f '(0) = 2 ∙ 0 = 0,
f '(1) = 2 ∙ 1 = 2,
f '(2) = 2 ∙ 2 = 4.
Таким образом, в точке
х = –0,5 функция
f(x) = х2
+ 2
убывает, в точке х = 0 сохраняет
скорость постоянной, а вточках х = 1, х = 2 – растёт. Причём
f '(2) ˃ f '(1)
поэтому можно сказать (не глядя на рисунок), что в
окрестности точки х = 2 график
функции
f(x) = х2
+ 2
идёт
вверх круче, чем вблизи точки х = 1.Задания к уроку 2
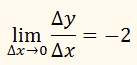
Комментариев нет:
Отправить комментарий