ВИДЕО УРОК
Будем рассматривать рациональные
тригонометрические уравнения относительно тригонометрических функций.
Рациональное уравнение
относительно тригонометрических функций одного и того же аргумента можно
записать в видегде R1, R2 – целые рациональные функции относительно
sin x, cos x, tg x, ctg x.
Если функции tg x и ctg x заменить
соответственно нато после преобразований уравнение сводится к виду
где R3 и R4 – целые рациональные функции относительно sin x, cos x.
Рассматривая это уравнение, приходим к выводу, что дробь может равняться
нулю, если числитель
R3(sin x, cos x) = 0, а знаменатель
R4(sin x, cos x) ≠
0.
Отметим, что R4(sin x, cos x) как многочлен от функций sin x и cos x – величина ограничена, так как
| sin x | ≤ 1 и | cos x | ≤ 1,
поэтому при всех значениях х
Что касается тех корней уравнения
R3(sin x, cos x) = 0,
при которых
R4(sin x, cos x) = 0,
то для уравнения
они являются посторонними из-за того, что левая часть уравнения
при этом приобретает вид
и не имеет числового смысла.
Таким
образом, в общем случае рациональные тригонометрические уравнения относительно
функций одного аргумента сводятся к уравнению вида
R(sin x, cos x) = 0,
где R – многочлен относительно
sin x и cos x.
Рассмотрим некоторые методы решения уравнения
R(sin x, cos x) = 0.
1. Один из методов заключается в применении так называемой универсальной тригонометрической подстановки, то есть формул, выражающих
sin x, cos x, tg x, ctg x
через tg x/2.
При применении этого метода уравнения
можно не сводить к виду
Функция tg x/2 не имеет смысла при
х = π(2n + 1)
где n = 0; ±1;
±2; …
поэтому при решении уравнения этим методом дополнительно следует проверить, нет ли среди значений
х = π(2n + 1)
корней данного уравнения.
ПРИМЕР:
Решить уравнение:
sin x – 2cos x = 2.
РЕШЕНИЕ:
Заменив с помощью формул:
получим
После преобразования получим уравнение
tg x/2 = 2.
с которого находим
x = 2 arctg 2 + 2πn,
где n = 0; ±1; ±2;
…
Допустимыми значениями неизвестного в данном уравнении были все действительные значения х. При переходе к функции tg x/2 по рассмотрению выпали значение
х = π(2n + 1),
подлежащих проверке по условию.
Подставляя
х = π(2n + 1)
в данное уравнение, убеждаемся, что эти значения являются решениями уравнения.
ОТВЕТ:
x = 2 arctg 2 + 2πn;
х = π(2n
+ 1),
где n = 0; ±1; ±2;
…
ПРИМЕР:
Решить уравнение:
1 – sin x = cos x (sin x + cos x).
РЕШЕНИЕ:
Выразив sin x и cos x через tg x/2, получим уравнение
которое после преобразований имеет вид:
и, поэтому,
х = 2πn или
х = π/2 + 2πn
(n = 0; ±1; ±2;
…).
Проверим, будут корнями данного уравнения значения
х = π(2n + 1).
Подставляя это значение в данное уравнение, находим
1 – sin [π(2n + 1)] = cos [π(2n + 1)]∙{(sin [π(2n + 1)] + cos [π(2n + 1)])}
или
1 – 0 = –1(0 – 1), 1 = 1,
то есть значение
х = π(2n + 1)
также являются корнями уравнения.
Таким образом корнями данного уравнения
будут значения, определенные по формулам:
х = 2πn
х = π/2 + 2πn,
х = π(2n
+ 1),
где n = 0; ±1; ±2;
…
отметим, что первая и третья формулы могут быть заменены на одну формулу
х = πn.
ОТВЕТ:
х = πn, х = π/2 + 2πn,
где n = 0; ±1; ±2;
…
2. Универсальная подстановка часто приводит к уравнению высокой степени относительно tg x/2 и поэтому неудобна. Иногда проще при решении уравнения пользоваться заменами:
Напомним, что
sin (–x) = – sin x,
cos (–x) =
cos x,
sin (π – x) = sin x,
cos (2π – x) = cos x.
Поэтому, если в уравнении левая часть не меняется при замене х на –х, или на π – х, то это означает, что она ведет себя как cos x и в этом случае целесообразно заменить
sin x на
Напротив, если при замене х на –х левая часть уравнения меняет только знак или если при замене х на π – х она не меняется, то целесообразно в уравнении оставить функцию sin x, то есть cos x заменить на
ПРИМЕР:
Решить уравнение:
3 sin3 x + 3 sin x cos2 x + 2 cos2 x = 0.
РЕШЕНИЕ:
Левая часть этого уравнения не является функцией ни чётной, ни нечетной. Поэтому проверяем поведение левой части уравнения при замене х на π – x. Убеждаемся, что при такой замене она не меняется. В этом случае целесообразно заменить
cos2 х на 1 – sin2х.
После замены получаем:
3 sin3 x + 3 sin x (1 – sin2х) + 2 (1 – sin2х) = 0
или
2 sin2 x – 3 sin x – 2 = 0.
Решая это квадратное уравнение относительно sin x, найдём:
sin x = 2, sin x = –1/2.
Первое из уравнений решений не имеет, а из другого получаем искомый ответ:
x = (–1)n+1 π/6 + πn,
где n = 0; ±1; ±2;
…
ПРИМЕР:
Решить уравнение:
4 sin4 x – 2 sin2 x cos x + 4 cos 2x
= 2 cos3 x
–
sin2 2х + 2.
РЕШЕНИЕ:
При замене х на –х обе части уравнения не изменяются. Поэтому целесообразно выполнить замену
Учитывая, что
sin 2x = 2 sin x cos x,
cos 2x = cos2
x – sin2 2х,
sin2 х = 1 – cos2 x,
получаем
4(1 – cos2 x)2 – 2(1 – cos2 x) cos x + 4(2 cos2 x – 1)
4 cos2 x – 2 cos x – 2 = 0,
2(2 cos2 x – cos x – 1) = 0,
2 cos2 x
– cos x – 1 = 0
откуда, решая последнее уравнение относительно cos x, находим
cos x = 1,
cos x = – 1/2.
Из этих уравнений получаем:
x = 2πn, х = ± 2π/3 + 2πn.
ОТВЕТ:
x = 2πn, х = ± 2π/3 + 2πn,
де n = 0; ±1; ±2;
…
3. Уравнение можно решать сведением до однородного тригонометрического уравнения относительно
sin x и cos x.
Однородным уравнением относительно sin x и cos x называют уравнение, каждый член которого имеет ту же степень относительно sin x и cos x.
ПРИМЕР:
Однородное уравнение второй степени относительно sin x и cos x имеет вид
а sin2 x + b sin x cos x + с cos2 x = 0.
Однородное уравнение второй степени относительно sin x и cos x имеет вид
а sin 2x + b sin x cos x + с cos 2x = 0.
Такое уравнение легко сводится к уравнению с одной неизвестной функцией делением обеих частей уравнения на cos2 x или sin2 x. После деления на cos2 x получаем квадратное относительно tg х уравнение
а tg2 x + b tg x + с = 0.
При дилении на cos2 x (или sin2 x) необходимо показать, что cos2 x ≠ 0. Действительно, подставив cos x = 0 в исходное уравнение, получим а sin2 x = 0, а это при а ≠ 0 невозможно, поскольку если cos x = 0, то sin x = 1.
Аналогично однородное относительно sin x
и cos x уравнение n-й степени
an sinnx + an-1sinn-1x cos x + …+ a1sin x cosn-1x + a0cosnx = 0
делением на cosn x или sinn x можно свести до алгебраического уравнения n-й степени относительно tg х или ctg х.
Уравнения всегда можно свести до однородного уравнения относительно sin x и cos x. Для этого достаточно члены четной степени перенести в
одну, а нечетной степени относительно sin x
и cos x –
в другую часть и возвести обе части уравнения в квадрат.
Далее, пользуясь тем, что при любом k
(sin2 x + cos2 x)k = 1,
показатель k подбирается так, чтобы уравнение стало однородным.
ПРИМЕР:
Сведем уравнение
2 sin2 x + cos x – 3 sin x + 1 = 0.
до однородного.
РЕШЕНИЕ:
Перепишем это уравнение в виде
2 sin2 x + 1 = 3 sin x – cos x.
обе его части возведем в квадрат, после чего получим
4 sin4 x + 4 sin2 x + 1 = 9 sin2 x – 6 sin x cos x + cos2 x.
Подобрав показатель k соответствующим образом, данное уравнение можно записать так:
4 sin4 x + 4 sin2 x(sin2 x + cos2 x) + 1(sin2 x + cos2 x)
= (9 sin2 x – 6 sin x cos x + cos2 x)(sin2 x + cos2 x).
Отсюда после очевидных преобразований получаем уравнение четвертой степени
3 sin3 x cos x – 2 sin2 x cos2 x + 3 sin x cos3 x = 0,
однородное относительно sin x и cos x.
ПРИМЕР:
Решить уравнение:
sec x = 4 sin x + 6 cos x.
РЕШЕНИЕ:
Умножив обе части уравнения на cos x ≠ 0, получим
1 = 4 sin x cos x + 6 cos2 x
и заменим
1 = sin2 x + cos2 x,
тогда имеем
sin2 x – 4 sin x cos x – 5 cos2 x = 0.
Последнее уравнение разделим на cos2 x, после чего получим:
tg2 х – 4 tg х – 5 = 0,
отсюда находим
tg х = 5, tg х = –1.
Итак,
х = arctg 5 + πn.
х = –π/4 +πn,
где n = 0; ±1; ±2;
…
ПРИМЕР:
Решить уравнение:
sin3 x – cos3 x + 1 = 0.
РЕШЕНИЕ:
Перенеся члены нечетной степени относительно sin x и cos x в одну часть, получим
cos3 x – sin3 x = 1.
Возведём обе части в квадрат и умножим 1 на
(sin2 x + cos2 x)3.
Уравнение примет вид
(cos3 x – sin3 x)2 = (sin2 x + cos2 x)3,
или
cos6 x – 2 cos3 x sin3 x + sin6
x –
sin6 x – 3 cos2
x sin4 x – 3 cos4 x sin2 x – cos6 x = 0,
3 sin4 x cos2 x + 2 sin3 x
cos3 x + 3 sin2
x cos4 x = 0,
или
3 sin2 x cos2 x + 2 sin3 x cos3 x = 0,
Раскладывая на множители, получаем:
sin2 x cos2 x (3 + 2 sin x cos x) = 0.
поскольку
3 + 2 sin x cos x ≠ 0,
то окончательно имеем
sin2 x = 0 и cos2 x = 0 и,
следовательно
х = πn,
х = π/2 (2n + 1).
Проверив найденные значения по условию уравнения, в ответе получим:
х = 2πk,
х = π/2 (4k – 1).
где k = 0; ±1; ±2;
…
4. Рассмотрим уравнение вида
а sin x + b cos x = с.
Коэффициенты а, b и с – произвольные действительные числа.
получим
Коэффициенты при sin x и cos x будем рассматривать как значение косинуса и синуса вспомогательного аргумента φ, то есть считать потому что Без ограничения общности можем полагать, что b ≥ 0, тогда
sin φ ≥ 0
угол можно взять в промежутке
0 < φ < π.
Определив по таблицам значение φ, данное уравнение запишем в виде
или Если то есть
а2 + b2 ≥ с2,
то решениями уравнения значения
где n = 0; ±1; ±2; … если то есть
а2 + b2 < с2,
то уравнение не имеет решений.
ПРИМЕР:
Решить уравнение:
√͞͞͞͞͞3 sin x + cos x = 1.
РЕШЕНИЕ:
Поделив обе части уравнения на 2, получим:
Заменим Тогда исходное уравнение примет видо ткуда следует
х + 30° = (–1)n ∙ 30° + 180°n,
n = 0; ±1;
±2; …
или при
n = 2k
n = 2k + 1
х = 180° ∙ 2k
х = –60° + 180°(2k + 1).
ОТВЕТ:
x = 360° k
x = 120°(3k + 1)
k = 0; ±1;
±2; …
5. Рассмотрим уравнение
sinn x + cosn x = 1,
где – n натуральное число.
Если n = 1, то уравнение приводится к виду, рассмотренному в пункте
4.
При n = 2 имеем
тождество
sin2 х + cos2 х = 1,
где х – любое действительное число.
При n ˃ 3, если
| sin x | ≠ 1,
| cos x | ≠ 1,
имеем
sinn x < sin2 х
cosn x < cos2 х
потому что показательная функция с основанием, меньше единицы, убывает. Добавляя почленно полученные неравенства, найдем, что
sinn x + cosn x < 1, n ≥ 3
при всех х, для которых
| sin x | ≠ 1,
| cos x | ≠ 1.
Таким образом, если n – нечётное число, то возможны случаи
из которых соответственно получаем решения данного уравнения
x = 2πk
x = π/2 (2k + 1)
k = 0; ±1; ±2;
…
если n – чётное число, то возможны случаи
из которых получаем решения данного уравнения
x = π/2 k
k = 0; ±1;
±2; …
ПРИМЕР:
Решить уравнение:
sin3 x + cos3 x = 1.
РЕШЕНИЕ:
Из изложенного выше следует, что уравнение может иметь решение в следующих двух случаях:
Откуда находим решения:
x = 2πk
x = π/2 (4k + 1)
ОТВЕТ:
x = 2πk
x = π/2 (4k + 1)
k = 0; ±1;
±2; …
При n ≥ 3 корни уравнения
sinn x + cosn x = 1
зависят не от численного значения величины n, а только от того, чётное n или нет.
Задания к уроку 2
ДРУГИЕ УРОКИ
- Урок 1. Простейшие тригонометрические уравнения
- Урок 3. Тригонометрические уравнений с функциями разных аргументов
- Урок 4. Графический метод решения тригонометрических уравнений
- Урок 5. Системы тригонометрических уравнений
- Урок 6. Тригонометрические неравенства
- Урок 7. Графическое решение тригонометрических неравенств





















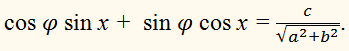










Комментариев нет:
Отправить комментарий