Прежде чем приступить к решению примеров и задач, обязательно ознакомьтесь с теоретической частью урока
Нахождение области определения и области значения функции аналитическим методом
1. Найдите область определения функции:
б) (–∞; 6);
в) (6; +∞);
г) [6; +∞);
г) [6; +∞);
2. Областью определения какой из функций будет промежуток ?
(–∞; 4).
б) (–∞; 8);
в) (8; +∞);
г) [8; +∞);
г) [8; +∞);
4. Какое значение х не входит в область определения функции ?
б) –2;
в) 0, 2;
5. Областью значения какой из данных функций будет одно число ?
а) {1; 2; 3};
б) {1;
2; 3; 4; 5};
в) {2;
3; 4};
г) {1;
2; 3; 4}.
7. Областью значения какой из данных функций будет промежуток вида [а; +∞), где а – некоторое отличное от нуля число ?
а) у =
√͞͞͞͞͞х;
б) у =
3х – 2;
в) у =
|х|;
8. Найдите область определения функции:
б) x ∈ [3; 6);
в) x ∈ (3; 6);
9. Областью определения какой из функций будет промежуток
(–∞; 7) ?
(–∞; –1) ∪ (–1; 2) ∪ (2; +∞) ?
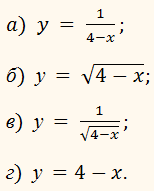
Комментариев нет:
Отправить комментарий