Урок 25. Графіки функцій y = sin x і y = cos x

понедельник, 18 марта 2019 г.

Урок 25. Графіки функцій y = sin x і y = cos x

ВІДЕО УРОК

Графік функції у = sin x.

Побудувати графік цієї функції можна двома способами.

Перший спосіб полягає в наступному: даємо значення аргументу х та знаходимо відповідні значення функції sin x. В результаті отримаємо наступну таблицю:

Далі, у прямокутній системі координат

будуємо точки, що відповідають знайденим парам значень х і sin x, користуючись однаковими масштабами по осях Ох та Оу.

На підставі вже встановлених властивостей функцій sin x ці точки можна поєднати плавною кривою і вийде частина графіка функції у = sin x.

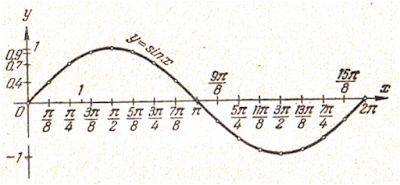
Надалі при побудові графіка функції у = sin x обмежуватимемося лише таблицею для п'яти перших точок:

(0; 0), (^π/₈; 0,4), (^π/₄; 0,7), (^3π/₈; 0,9), (^π/₂; 1).

Наступні чотири точки виходить на підставі формули

sin (^π/₂ + α) = sin (^π/₂ – α)

яка показує, що графік функції у = sin x симетричний щодо прямої, що проходить через точку осі Ох з абсцисою ^π/₂ та паралельної осі Оу.

Формула

sin (π + α) = –sin α

показує, що точка (π; 0) є центром симетрії синусоїди (це підтверджує таблицю). Сказане дає можливість побудувати другу половину кривої хвилі, розташовану під віссю Ох.

На підставі періодичності функції sin x отриманий графік може бути продовжений як ліворуч, так і праворуч.

Інший спосіб побудови графіка функції у = sin x – геометричний.

Розіб'ємо одиничне коло на довільне число рівних частин (наприклад на 16)

і помітимо кінці дуг відповідно до значень

0, ^π/₈, ^π/₄, ^3π/₈, …, 2π.

Побудуємо ординати точок поділу, тобто синуси відповідних дуг. Слід звернути увагу на те, що синуси дуг, що закінчуються в точках, симетричних щодо осі Оу, між собою рівні, тому що за формулами наведення маємо:

На підставі цього можна обмежитись (що на практиці і робиться) побудовою ординат точок правого півкола.

Нехай тепер дане коло розрізане в точці з нульовим розподілом, спрямоване і відкладене (разом з нанесеними на ньому поділами) вправо від точки О'у напрямку осі абсцис. Для цього достатньо 16 разів відкласти відрізок завдовжки

^2π/₁₆ = ^π/₈ ≈ 0,4.

обраної одиниці (нагадаємо, що радіус одиничного кола дорівнює одиниці довжини, і тому довжина всього кола дорівнює 2π, а довжина її шістнадцятої частини дорівнює π/8).

Приймемо точку О' за початок нової системи координат. Нову вісь абсцис О'х направимо старою Ох. Нову вісь ординат О'у направимо паралельно старої Оу.

Після цього з точок поділу спрямленого кола ми відновимо промені, перпендикулярні до осі Ох і спрямовані вгору для значень

0 ≤ х ≤ π

і вниз для

π ≤ х ≤ 2π.

Відкладемо ними відповідні значення ординат, взяті з кола. Кінці цих перпендикулярів визначаються своїми координатами: абсциса – дуга, ордината – синус. Побудову перпендикулярів можна замінити простим паралельним перенесенням відповідних ординат, проведених у колі. Таким чином, отримуємо низку точок. Поєднавши їх плавною лінією, отримаємо графік синусоїди.

Частина синусоїди, що відповідає одному повному обороту рухомого радіусу, наприклад, взята в проміжку між 0 і 2π, називається хвилею. Її становлять дві напівхвилі, два <<горби>>. Відрізок осі О'х, на який спирається напівхвиля синусоїди, називають базою синусоїди. Завдяки тому, що масштаб по осях О'х і О'у' нами взятий однаковий, між максимальною її ординатою, що дорівнює одиниці, і базою, що дорівнює π ≈ 3,14, існує певне співвідношення: база синусоїди в π разів більша за її максимальну ординату .

Синусоїда є суцільною, без розривів, кривою лінією.

Графік функції у = sin x дозволяє наочно простежити властивості цієї функції:
проміжки, у яких функція зростає одночасно зі зростанням аргументу

проміжки, у яких функція зменшується зі зростанням аргументу

значення аргументу

при яких функція набуває максимальних значень (+1);
значення аргументу

при яких функція набуває мінімальних значень (–1);

значення аргументу (kπ), у яких функція перетворюється на нуль (точки перетину графіка з віссю Ох) тощо (k – будь-яке ціле число).

Розглянемо ще один спосіб побудови графіка у = sin x.

Візьмемо контрольні точки

(0; 0), (^π/₆; ¹/₂), (^π/₂; 1), (π; 0),

побудуємо напівхвилю – графік функції у = sin x на відрізку [0; π].

Оскільки функція у = sin x непарна, то виконавши симетрію побудованого графіка щодо початку координат, отримаємо графік функції на відрізку [–π; π].

Нарешті, скориставшись періодичністю функції у = sin x, можна побудувати графік по всій області визначення.

Графік функції у = sin x дозволяє вловити деякі тонкощі зміни цієї функції. Наприклад, крива при виході з початку координат досить круто піднімається вгору, ординати її значно зростають у разі зростання абсцис: у міру наближення аргументу до ^π/₂(90°) ординати ростуть повільно, підйом кривої мало помітний. Такі відмінності у характері зміни sin x поблизу нуля та поблизу ^π/₂пояснюють нам, чому табличні різниці для синусів у тригонометричних таблицях зменшуються в міру наближення аргументу до ^π/₂ (у той час як табличні різниці кутів поблизу нуля при зміні їх на 1' рівні 0,0003, ці ж різниці поблизу ^π/₂ виражаються частками, меншими 0,0001).

Деякі властивості функції у = sin x.

1. Область визначення – безліч всіх дійсних чисел.

2. Область значень – відрізок [-1; 1].

3. Функція періодична, основний період дорівнює 2π.

4. Безперервність функції у = sin x.

Функція у = sin x існує при всіх дійсних значеннях х, причому графік є суцільною кривою лінією (без розривів), тобто функція у = sin x безперервна.

5. Функція у = sin x непарна, та її графік симетричний щодо початку координат.

6. Найбільші та найменші значення. Усі можливі значення функції у = sin x обмежені нерівностями

–1 ≤ sin x ≤ +1,

причому

sin x = +1,

якщо х = ^π/₂ + 2πn, і

sin x = –1,

якщо х = ^3π/₂ + 2πn,

де n = 0; ±1; ±2; …

7. Нульові значення (точки перетину графіка функції з віссю абсцис).

sin x = 0,

якщо х = πn,

(n = 0; ±1; ±2; …).

8. Інтервали зростання та спадання.

З графіка функції у = sin x
видно і з визначення цієї функції випливає, що при зміні х від

–^π/₂ + 2πn ≤ x ≤ ^π/₂ +2πn

(n = 0; ±1; ±2; …)

функція sin x зростає від –1 до +1, приймаючи всі проміжні значення.

Це означає, що більшому значенню кута х із цього проміжку відповідає більше значення sin x, тобто якщо

–^π/₂ ≤ х₁ < х₂ ≤ ^π/₂

то

–1 ≤ sin х₁ < sin х₂ ≤ +1

такий кут х, і до того ж єдиний, синус якого дорівнює у.

При зміні х від ^π/₂ до ^3π/₂ функція sin x зменшується від +1 до –1, тобто більшого значення х із цього проміжку відповідає менше значення sin x. При зміні х від ^π/₂ до ^3π/₂ функція sin x зменшується від +1 до –1, тобто більшому значенню х із цього проміжку відповідає менше значення sin x. При цьому sin x набуває всіх проміжних значень між +1 и –1.

Період функції sin x дорівнює 2π. Тому можна до меж розглянутого проміжку додати по 2πn.

^π/₂ + 2πn ≤ x ≤ ^3π/₂ +2πn

(n = 0; ±1; ±2; …)

Графік функції у = соs x.

Формулу приведення

соs x = sin (^π/₂ + х)

можна прочитати так: косинус будь-якого кута дорівнює синусу кута, на ^π/₂ більшого, так що маємо:

соs 0 = sin ^π/₂, соs ^π/₈ = sin ^5π/₈,

соs ^π/₄ = sin ^3π/₄, соs ^3π/₈ = sin ^7π/₈,

соs ^π/₂ = sin π, соs ^5π/₈ = sin ^9π/₈.

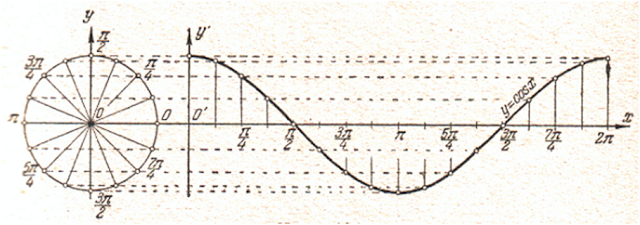
На підставі поміченого властивості функції соs x побудова графіка цієї функції зводиться до наступного.

Візьмемо таку саму одиничну коло, як із побудові графіка функції у = sin x, і розділимо їх у 16 рівних частин

На осі Ох точку О' приймемо початок нової прямокутної системи координат; при цьому напрямок нової осі абсцис О'х збігається з напрямком осі Ох, а нова вісь ординат О'у' проходить паралельно осі Оу.

Від точки О' вправо по осі О'х відкладемо 16 рівних частин, кожна з яких дорівнює 1/16 довжини одиничного кола. Кінці поділів зліва направо позначені числами:

^π/₈, ^π/₄, ^3π/₈,^π/₂, …, 2π.

Точці О' відповідає нульовий поділ. Далі слід знайти ординати графіка функції соs x, відповідні поміченим абсцис. Ось тут і використовується рівність значень

соs x и sin (^π/₂ + х).

Поступаємо наступним чином. Переносимо по порядку паралельні ординати кінців наступних дуг кола

^π/₂, ^5π/₈, ^3π/₄, ^7π/₈, π, …

у відповідні точки, що мають на осі О'х абсциси:

0, ^π/₈, ^π/₄, ^3π/₈, ^π/₂, …

Кожній парі отриманих значень абсциси та ординати відповідає єдина точка, що належить графіку функції

у = соs x.

Поєднавши побудовані точки плавною лінією, отримаємо графік косинусоїди. Косинусоїда є синусоїдою, зміщену вздовж осі О'х вліво на ^π/₂.

З цього укладаємо, що графік функції у = соs x то, можливо отримано наступним чином.

Будуємо в деякій прямокутній системі координат з осями Ох та Оу графік функції у = sin x; після цього переносимо початок координат у точку О'(^π/₂, 0) і приймаємо за нову вісь абсцис пряму О'х, позитивний напрямок якої збігається з позитивним напрямом осі Ох, а за нову вісь ординат пряму О'у', паралельну Оу.

Будь-яка ордината цієї кривої виражає собою синус кута, відрахованого по осі Ох від точки, або косинус кута, відрахованого по осі О'х від точки О'.

З графіка функції у = соs x видно, що соs x зменшується від 1 до –1 на будь-якому проміжку зростання х від 2kπ до π + 2kπ і зростає від –1 до +1 на будь-якому проміжку зростання х від 2kπ + π до 2(k + 1)π; соs x приймає максимальні значення (+1) при х = 2kπ та мінімальні значення (–1) при х = π + 2kπ; соs x при х = ^π/₂ + kπ перетворюється на нуль (k – будь-яке ціле число).

Графік функції у = cos x легко одержати з графіка функції у = sin x.

За будь-якого х, згідно з формулою, маємо

y = cos x = sin (x + ^π/₂).

Отже, замість значення косинуса можна взяти значення синуса, збільшивши аргумент на ^π/₂, тобто графіком функції y = cos x служить той самий синусоїда, але пересунута на ^π/₂ вліво по осі абсцис.

Деякі властивості функції y = cos x.

1. Область визначення – безліч всіх дійсних чисел.

2. Область значень – відрізок [–1; 1].

3. Функція періодична, основний період дорівнює 2π.

4. Функція y = cos x парна, та її графік симетричний щодо осі ординат.

5. Найбільші та найменші значення. Усі можливі значення функції у = cos x обмежені нерівностями

–1 ≤ cos x ≤ +1,

причому

cos x = +1,

якщо х = 2πn, и

cos x = –1,

якщо х = (2n + 1)πn,

де n = 0; ±1; ±2; …

6. Нульові значення (точки перетину графіка функції з віссю абсцис).

cos x = 0,

якщо х = ^π/₂ (2n + 1),

(n = 0; ±1; ±2; …).

7. Інтервали зростання та спадання.

З графіка функція у = cos x
видно і з визначення її слід, що з зміні аргументу х від 0 до π функція cos x зменшується від +1 до –1, приймаючи все проміжні значення. Це означає, що:

більшого значення з цього проміжку відповідає менше значення cos x, тобто якщо

0 ≤ х₁ < х₂ ≤ π

то

+1 ≥ cos х₁ > cos х₂ ≥ –1.

Будь-якому значенню функції у, що задовольняє нерівності

–1 ≤ у ≤ +1,

відповідає єдине значення аргументу х, що задовольняє нерівності

π ≥ х ≥ 0,

таке, що

cos x = у.

При зміні х від π до 2π. При цьому cos x набуває всіх проміжних значень від –1 до +1.

Період функції соs x дорівнює 2π. Тому можна до меж розглянутого проміжку додати по 2πn.

π + 2πn ≤ x ≤ 2π +2πn

(n = 0; ±1; ±2; …)

Завдання до уроку 25

Інші уроки:

Уроки математики и физики для школьников и родителей

понедельник, 18 марта 2019 г.