ВІДЕО УРОК
У кожному трикутнику відношення сторони до синуса протилежного
кута є постійна величина (для даного трикутника), що дорівнює довжині діаметра описаної біля
трикутника кола.
Або, іншими словами:
∠ А,
∠ В, ∠ С.
Оскільки CD = 2R і ∠ BDC
= ∠ BAC
= A, то з
прямокутного трикутника CBD маємо:
а
= 2R sin A.
Припустимо, що у трикутнику АВСкут А – тупий. Тоді проводимо діаметр СD і з'єднуємо вершину трикутника АВС з точкою D. З прямокутного трикутника ВСD знаходимо:
BC
= CD sin ∠ BDC.
Але кут ВDС
у сумі з кутом А становить 180°
як протилежні кути опуклого
чотирикутника, вписаного в коло, а тому
∠ BDC = 180° – A.
Тому
BC
= CD sin ∠ (180° – A),
або
a
= 2R sin A.
Ряд рівних відносин може бути записаний і так:
a
:
b : c = sin A : sin B
: sin C.
Запишемо формули для обчислення площі даного трикутника:ЗвідсиТодіабоЗ цих рівностей випливає:Отже, доведено теорему, яка називається теоремою синусів:
ЗАДАЧА:
Радіус
кола, описаного навколо трикутника АВС, дорівнює 6
см. Знайдіть радіус кола, описаного навколо трикутника АОС,
де О
– точка перетину бісектрис трикутника АВС, якщо ∠ АВС = 60°.
РОЗВ'ЯЗАННЯ:
ЗАДАЧА:
На
стороні ВС
трикутника АВС
позначили точку D.
Знайдіть відрізок ВD, якщо
∠ С = 90°,
∠ ВАС
= α,
∠ ВАD
= β,
АВ = с.
РОЗВ'ЯЗАННЯ:
Трикутник АВС
– заданий,
∠ В = 90° – α.
∠ ВDА
= 180° – β – (90° – α) =
= 90° + α – β.
Відрізок
AD – бісектриса трикутника АВС,
АD = а,
∠ С = 90°,
∠ ВАС = α.
Знайдіть
відрізок ВD.
РОЗВ'ЯЗАННЯ:
ВD
– бісектриса кута А, тому
∠ В = 90° – α.
Основа
трикутника дорівнює 10 см, один з кутів при основі
дорівнює 45°, а кут, що проти лежить основі,
дорівнює 60°. Знайдіть сторону, що протилежна
куту в
45°.
РОЗВ'ЯЗАННЯ:
У
трикутнику АВС:
∠ А = 45°,
∠ С = 15°,
ВС = 4√͞͞͞͞͞6.
Знайти АС.
РОЗВ'ЯЗАННЯ:
Користуючись
теоремою про суму кутів трикутника
∠ А + ∠ В + ∠ С = 180°,
Знайдемо
кут В:
∠ В = 180° – 45° – 15° = 120°.
ЗАДАЧА:
У
трикутнику КМN:
∠ K = 80°,
∠ N = 40°,
КN = 6 см.
Знайти радіус кола, описаного біля
трикутника.
РОЗВ'ЯЗАННЯ:
З
теореми про суму кутів трикутника знайдемо невідомий кут трикутника:
∠ М = 180° – ∠ К – ∠ N.
Підставляючи
значення відомих кутів, отримаємо:
∠ М = 180° – ∠ 80° – ∠ 40°,
∠ М = 60°.
ЗАДАЧА:
Гіпотенуза
та один із катетів прямокутного трикутника дорівнюють 10
см та 8
см. Знайти кут, який розташований проти даного катета.
РОЗВ'ЯЗАННЯ:
х
≈ 53,1°.
- Урок 1. Градусний вимір кутових величин
- Урок 2. Радіанне вимірювання кутових величин
- Урок 3. Основні тригонометричні функції
- Урок 4. Натуральні тригонометричні таблиці
- Урок 5. Періодичність тригонометричних функції
- Урок 6. Область визначення і область значення тригонометричних функцій
- Урок 7. Знаки тригонометричних функцій
- Урок 8. Парність і непарність тригонометричних функцій
- Урок 9. Тригонометричні функції деяких кутів
- Урок 10. Побудова кута за даним значенням його тригонометричної функції
- Урок 11. Основні тригонометричні тотожності
- Урок 12. Вирази всіх тригонометричних функцій через одну з них
- Урок 13. Розв'язання прямокутних і рівнобедрених трикутників за допомогою тригонометричних функцій
- Урок 15. Теорема косинусів
- Урок 16. Рішення косокутних трикутників
- Урок 17. Приклади рішення завдань з планіметрії із застосуванням тригонометрії
- Урок 18. Рішення практичних завдань за допомогою тригонометрії
- Урок 19. Формули зведення (1)
- Урок 20. Формули зведення (2)
- Урок 21. Формули додавання і віднімання аргументів тригонометричних функцій
- Урок 22. Формули подвійних і потрійних кутів (аргументів)
- Урок 23. Формули половинного аргументу
- Урок 24. Формули перетворень суми тригонометричних функцій в добуток
- Урок 25. Графіки функції y = sin x і y = cos x
- Урок 26. Графіки функції y = tg x і ctg x
- Урок 27. Обернені тригонометричні функції
- Урок 28. Основні тотожності зворотних тригонометричних функцій
- Урок 29. Вираз одній з аркфункцій через інші
- Урок 30. Графіки зворотних тригонометричних функцій
- Урок 31. Побудова графіків тригонометричних функцій методом геометричних перетворень



























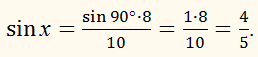
Комментариев нет:
Отправить комментарий