To graph a linear function:
1. Find 2 points which satisfy the equation
2. Plot them
3. Connect the points
with a straight line
EXAMPLE:
y = 25 + 5x
SOLUTION:
Let x = 1 then
y = 25 + 5(1) = 30
Let x = 3 then
y = 25 + 5(3) = 40
EXAMPLE:Draw the straight line
y = x + 3.
When working out the y-values,
we usually write them in a table
Have you ever seen sighs like this?
This is the gradient – how steep the hill is.
The steeper the hill, the bigger the gradient.
EXAMPLE:
Find the gradient of this line.
Find the gradient of this line.
If a line slopes downwards to the right, it has a negative gradient.
The slope of a linear function
The steepness of a hill is called a slope. The same goes for the steepness of a line. The slope is defined as the ratio of the vertical change between two points, the rise, to the horizontal change between the same two points, the run.
It is important to keep the x-and y-coordinates in the same order in both the numerator and the denominator otherwise you will get the wrong slope.
EXAMPLE:
Find the slope of the line
A line with a positive slope (m ˃ 0), as the line above, rises from left to right whereas a line with a negative slope (m < 0) falls from left to right,
If two lines have the same slope the lines are said to be parallel.
y = mx + b
Lesson 18
Gradient
Have you ever seen sighs like this?
This is the gradient – how steep the hill is.
The “1 in 10” means that the hill goes up 1 m for every 10
m across.
Gradient = 1 in 10 = 1/10The steeper the hill, the bigger the gradient.
EXAMPLE:
Find the gradient of this line.
Find the gradient of this line.
If a line slopes downwards to the right, it has a negative gradient.
The slope of a linear function
The steepness of a hill is called a slope. The same goes for the steepness of a line. The slope is defined as the ratio of the vertical change between two points, the rise, to the horizontal change between the same two points, the run.
It is important to keep the x-and y-coordinates in the same order in both the numerator and the denominator otherwise you will get the wrong slope.
EXAMPLE:
Find the slope of the line
A line with a positive slope (m ˃ 0), as the line above, rises from left to right whereas a line with a negative slope (m < 0) falls from left to right,
If two lines have the same slope the lines are said to be parallel.
You can express a linear function using the slope
intercept form.
y = mx + b
m = slope
b = y – intercept
Lesson 18


















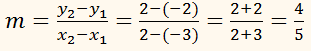


Комментариев нет:
Отправить комментарий