Функции у = √͞͞͞͞͞х и её свойства .
Разберем функцию.
Так как х лежит под корнем,
то он может принимать только неотрицательные значения. То есть он должен быть
больше или равен нулю.
– область определения – луч [0;
+ ∞),
это следует из того, что выражение √͞͞͞͞͞х определено лишь при х
≥ 0;
–
множество значений функции является
промежуток [0;
+ ∞);
–
значение функции у
= 0 является
наименьшим, а наибольшего значения функция не имеет;
– функция у = √͞͞͞͞͞х ни чётная, ни нечётная;
–
функция непериодическая;
–
точка (0; 0) является
нулём функции;
– функция у = √͞͞͞͞͞х монотонно возрастает на области определения [0; + ∞).
–
функция принимает положительные значения
на промежутке [0;
+ ∞).
ПРИМЕР:
Откуда х = 1, тогда у = 1, поэтому точка пересечения (1; 1).
ОТВЕТ: графики
пересекаются в точке (1; 1)
ПРИМЕР:
ОТВЕТ: графики
пересекаются в точке (1; 1)
ПРИМЕР:
График функции состоит из
части прямой у = х + 2 для х
≤ –1,
части параболы у = х2 для –1< х < 1 і
части графика функции у = √͞͞͞͞͞х для х ≥
1.
Функция растет на промежутках (–∞; –1] и [0; +∞) и падает на промежуток [–1; 0].
ОТВЕТ:
промежутки роста – (–∞; –1] и [0; +∞),
Постройте в одной системе координат графики функций
у = √͞͞͞͞͞x и
у = 6 – х.
С помощью графиков укажите значения х,
при которых значения функции у = 6 – х больше
значения функции у = √͞͞͞͞͞x .
РЕШЕНИЕ:
Пусть √͞͞͞͞͞x = t > 0. Получим:
6 – t2 = t,
t2 + t – 6 = 0,
t1 = –3 не
удовлетворяет условию t > 0,
t2 = 2, √͞͞͞͞͞x = 2,
х = 4, у
= 2,
А(4; 2).
Значение функции у = 6 – х больше значений функции у
= √͞͞͞͞͞x,
если х ∈ [0; 4).
Постройте в одной системе координат графики функций
у = √͞͞͞͞͞x и у = 2 – х.
С помощью графиков укажите значения х,
при которых значения функции у = √͞͞͞͞͞x больше
значения функции у = 2 – х.
РЕШЕНИЕ:
ПРИМЕР:
Решите графически уравнение
√͞͞͞͞͞x = 8/х.
РЕШЕНИЕ:
ПРИМЕР:
Решите графически уравнение
√͞͞͞͞͞x = 1/х.
РЕШЕНИЕ:
– область
определения функции – вся числовая прямая;
и график её напоминает график функцииПРИМЕР:
При каком значении а график функции
у = ах-3
проходит через точку
А (3; 1/54) ?
РЕШЕНИЕ:
у = ах-3.
Если график проходит через
точку А(3; 1/54), то:
1/54 = а ∙ 3-3,
1/54 = а ∙ 1/27, а =
0,5.
ПРИМЕР:
При каком значении а график функции
у = ах-5
проходит через точку
В (1/2; 192) ?
РЕШЕНИЕ:
у = ах-3.
Если график проходит через
точку В(1/2; 192), то:
192 = а ∙ (1/2)-5,
- Урок 1. Координатная плоскость
- Урок 2. Диаграммы
- Урок 3. Графики
- Урок 4. Множества
- Урок 5. Что такое функция ?
- Урок 6. Аналитический способ задания функции
- Урок 7. Табличный способ задания функции
- Урок 8. Графический способ задания функции
- Урок 9. Нахождение области определения и области значения функции аналитическим методом
- Урок 10. Нахождение области определения и области значения функции с помощью графика
- Урок 11. Нули функции
- Урок 12. Возрастание и убывание функции
- Урок 13. Экстремальные значения функции
- Урок 14. Симметричные функции
- Урок 15. Чётные и нечётные функции
- Урок 16. Функция, обратная данной
- Урок 17. Линейная функция
- Урок 18. График линейной функции
- Урок 19. Прямая пропорциональность
- Урок 20. График прямой пропорциональности
- Урок 21. Взаимное расположение графиков линейных функций
- Урок 22. Функция обратно пропорциональной зависимости
- Урок 23. График функции обратно пропорциональной зависимости
- Урок 24. Квадратичная функция
- Урок 25. График функции у = aх2 + b
- Урок 26. График функции у = a(х - m)2 + n
- Урок 27. График функции у = aх2 + bx + c
- Урок 29. Функция y = хn и её график
- Урок 30. Построение графиков функций методом геометрических преобразований






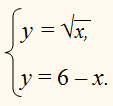






Комментариев нет:
Отправить комментарий