ВІДЕО УРОК
При рішенні геометричних завдань
векторним методом рекомендується користуватися наступною схемою.
наступні вектори:
РОЗВ'ЯЗАННЯ:
а) Зробимо складання за правилом трикутника, отримаємо:
З першого правила різниці двох векторів, отримуємо:
б) Оскільки
отримаємо
або
Використовуючи правило трикутника, остаточно отримаємо:
Обчислити обсяг піраміди, побудованої на векторах:
РОЗВ'ЯЗАННЯ:
Знайдемо мішаний добуток заданих векторів, для цього складемо визначник, по рядках якого запишемо координати векторів:
2 × 4 × 7 + 1 × 5 × 5 + 3 × 4 × 3 – 3 × 4 × 5 – 5 × 4 × 2 – 1 × 3 × 7 = –4.
ЗАДАЧА:
У кубі ADCDA1B1C1D1 точки Е і К – середини ребер відповідно A1B1 і B1C1. Знайдіть косинус кута між прямими АЕ і ВК.
РОЗВ'ЯЗАННЯ:
Куб добре вписується в прямокутну систему координат. Будуємо креслення.
Довжина ребра куба не дана. Якою б вона не була, кут між АЕ і ВК від неї не залежить. Тому візьмемо одиничний куб, всі ребра якого рівні 1.
Прямі АЕ і ВК – схрещуються. Для знаходження кута між векторами
треба знайти їх координати:
А(0; 0; 0),
Запишемо координати векторів:
Знайдемо косинус кута між векторами:
Скористаємося формулою:
Тоді
ВІДПОВІДЬ: cos φ = 4/5
ЗАДАЧА:
У правильної чотирикутної піраміді SABCD, всі ребра якої рівні 1, точки Е, К – середини ребер SB і SC відповідно. Знайдіть косинус кута між прямими АЕ і ВК.
РОЗВ'ЯЗАННЯ:
Виберемо початок координат в центрі підстави піраміди, а осі Х і Y накреслив паралельно сторонам підстави.
Знаходимо координати точок А, В, С.
Точка Е – середина SB, а К – середина SC. Скористаємося формулою для координат середини відрізка і знайдемо координати точок Е і К.
Знайдемо координати векторів Знайдемо косинус кута між ними.
Скористаємося формулою: Тоді ВІДПОВІДЬ: cos φ = 2/3
Запишемо координати точок:
Точка D – середина A1B1. Користуючись формулами для координат середини відрізка, знаходимо:
Знайдемо координати векторів
А потім косинус кута між ними:
Скористаємося формулою: Тоді ВІДПОВІДЬ:
Провести аналіз умови завдання:
– з'ясувати в якій системі координат
(двовимірною або тривимірною) розглядається це завдання;
– записати, що нам дане, що
треба знайти або довести, а також
побудувати креслення по умові завдання.
Перевести умову завдання і вимоги до
векторного виду. Скласти векторні співвідношення, що відповідають тому, що дано
в завданні і привести їх до векторних співвідношень, що відповідають вимогам
завдання. Перекласти отриманий результат геометричною мовою.
ПРИКЛАД:
Нехай даний паралелограм ABCD, діагоналі якого
перетинаються в точці О.
Виразити
через векторинаступні вектори:
РОЗВ'ЯЗАННЯ:
а) Зробимо складання за правилом трикутника, отримаємо:
З першого правила різниці двох векторів, отримуємо:
б) Оскільки
отримаємо
або
Використовуючи правило трикутника, остаточно отримаємо:

ЗАДАЧА:
Обчислити обсяг піраміди, побудованої на векторах:
РОЗВ'ЯЗАННЯ:
Знайдемо мішаний добуток заданих векторів, для цього складемо визначник, по рядках якого запишемо координати векторів:
2 × 4 × 7 + 1 × 5 × 5 + 3 × 4 × 3 – 3 × 4 × 5 – 5 × 4 × 2 – 1 × 3 × 7 = –4.
ЗАДАЧА:
У кубі ADCDA1B1C1D1 точки Е і К – середини ребер відповідно A1B1 і B1C1. Знайдіть косинус кута між прямими АЕ і ВК.
РОЗВ'ЯЗАННЯ:
Куб добре вписується в прямокутну систему координат. Будуємо креслення.
Довжина ребра куба не дана. Якою б вона не була, кут між АЕ і ВК від неї не залежить. Тому візьмемо одиничний куб, всі ребра якого рівні 1.
Прямі АЕ і ВК – схрещуються. Для знаходження кута між векторами
треба знайти їх координати:
А(0; 0; 0),
В(1;
0; 0),
Е(1/2;
0; 1),
К(1;
1/2;
1).
Запишемо координати векторів:
Знайдемо косинус кута між векторами:
Скористаємося формулою:
Тоді
ВІДПОВІДЬ: cos φ = 4/5
ЗАДАЧА:
У правильної чотирикутної піраміді SABCD, всі ребра якої рівні 1, точки Е, К – середини ребер SB і SC відповідно. Знайдіть косинус кута між прямими АЕ і ВК.
РОЗВ'ЯЗАННЯ:
Виберемо початок координат в центрі підстави піраміди, а осі Х і Y накреслив паралельно сторонам підстави.
Знаходимо координати точок А, В, С.
А(1/2; –1/2; 0),
В(1/2; 1/2; 0),
С(–1/2; –1/2; 0).
З прямокутного трикутника AOS знайдемо
Координати
вершини пірамідіТочка Е – середина SB, а К – середина SC. Скористаємося формулою для координат середини відрізка і знайдемо координати точок Е і К.
Знайдемо координати векторів Знайдемо косинус кута між ними.
Скористаємося формулою: Тоді ВІДПОВІДЬ: cos φ = 2/3
Покажемо тепер, як
вписати систему координат в трикутну призму.
ЗАДАЧА:
У
правильній трикутній призмі ABCA1B1C1,
всі ребра якої рівні 1, точка D
– середина ребра A1B1. Знайдіть косинус кута між прямими AD і BC1.
РОЗВ'ЯЗАННЯ:
Нехай точка А –
початок координат. Візьмемо вісь Х паралельно
стороні ВС, а
вісь Y перпендикулярно її. Іншими словами, на осі
буде лежати відрізок АН, який є висотою трикутника АВС. Намалюємо окремо нижня частина призми.
Запишемо координати точок:
А(0;
0; 0),
А1(0; 0; 1),Точка D – середина A1B1. Користуючись формулами для координат середини відрізка, знаходимо:
Знайдемо координати векторів
А потім косинус кута між ними:
Скористаємося формулою: Тоді ВІДПОВІДЬ:
Завдання до уроку 7































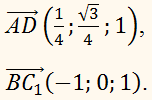




Комментариев нет:
Отправить комментарий