ВИДЕО УРОК
Основні
поняття, пов'язані з рішенням нерівностей з однією змінною.
Нехай дана нерівність
f(x) ˃ g(x).
Всяке значення змінної х, при якому ця
нерівність, звертається у вірну числову нерівність, називають рішенням
нерівності.
Розв’язати нерівність
– це означає знайти всі її розв’язки, або показати, що їх немає.
Дві нерівності називають рівносильними, якщо
вони мають одні й ті самі розв’язки, тобто якщо кожний розв’язок першої
нерівності задовольняє другу, а кожний розв’язок другої нерівності задовольняє
першу.
Нерівності, що не мають рішень, також вважаються
рівносильними.
При рішенні нерівностей зазвичай замінюють цю
нерівність іншим, простішим, але рівносильним цій нерівності. Потім отриману
нерівність знову замінюють простішим, рівносильним цій нерівності і так далі.
Лінійні
нерівності з однією змінною.
Лінійним називається нерівність виду ах
> b (або
відповідно ах < b, ах ≥
b, ах ≤ b), де а ≠ 0 и b – числа.
Рішенням нерівності з однією змінною називається
безліч таких значень змінної, які звертають його в правильне числове
нерівність.
0 × х > b,
тобто воно не має рішення при b
≥ 0 вірно при будь-яких х, якщо
b
< 0.
У лінійних нерівностях коефіцієнт при змінній не
дорівнює нулю. Може статися, що при рішенні нерівності може вийти нерівність
виду
0 × х > b або 0
× х
< b.
Нерівність такого виду, тобто і відповідна початкова
нерівність або не має рішень, або їх рішенням є будь-яке число.
Багато нерівностей в процесі перетворень зводяться
до лінійних нерівностей.
Властивості
нерівності.
– якщо з однієї
частини нерівності перенесемо в іншу доданок з протилежним знаком, то дістанемо
нерівність, рівносильну даній;
– якщо обидві частини нерівності помножимо або
поділимо на одне й те саме додатне число, то дістанемо нерівність, рівносильну
даній;
Нерівність
18 + 6х ˃ 0
рівносильна
нерівності
6х ˃ –18,
а
нерівність
6х ˃ –18
рівносильна
нерівності
х
˃ –3.
ПРИКЛАД:
Розв'яжіть
нерівність:
16х ˃ 13х + 45.
РОЗВ'ЯЗАННЯ:
Перенесемо
доданок 13х з протилежним знаком в ліву частину
нерівності:
16х – 13х ˃ 45.
Приведемо
подібні члени:
3х ˃ 45.
Розділимо
обоє дві частини нерівності на 3:
х
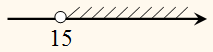
˃ 15.
Безліч
рішень нерівності складається з усіх чисел, великих 15.
Ця множина є числовим проміжком
(15; +∞),
ПРИКЛАД:
Розв'яжіть
нерівність:
15х – 23(х + 1) > 2х + 1.
РОЗВ'ЯЗАННЯ:
Розкриємо
дужки в лівій частині нерівності:
15х – 23х – 23 > 2х + 1.
Перенесемо
з протилежними знаками доданок 2х
з правої частини нерівності в ліву частину, а доданок –23
з лівої частини
в праву і приведемо подібні члени:
15х – 23х – 2х
> 23 + 11,
–10х >
34.
Розділимо
обидві частини на –10, при цьому змінимо знак нерівності
на протилежний:
(–∞; –3,4).
ВІДПОВІДЬ: (–∞;
–3,4)
ПРИКЛАД:
Розв'яжіть нерівність:
2(х – 3) + 5(1 – х) ≥ 3(2х – 5).
РОЗВ'ЯЗАННЯ:
Розкривши
дужки, отримаємо:
2х – 6 + 5 – 5х
≥ 6х – 15,
–3х – 1 ≥
6х – 15,
–3х – 6х ≥ –15 + 1,
–9х ≥ –14.
Розділимо
обидві частини нерівності на негативне число
–9
і змінимо знак нерівності.
Отримаємо
наступну нерівність, рівносильну первинній нерівності:
х
≤
14/9.
Безліч
рішень заданої нерівності буде промінь:
(–∞; 14/9].
ВІДПОВІДЬ: (–∞; 14/9]
ПРИКЛАД:
Розв'яжіть нерівність:
2(х + 8) –
5х < 4 – 3х.
РОЗВ'ЯЗАННЯ:
Маємо:
2х + 16 –
5х < 4 – 3х,
2х – 5х + 3х
< 4 – 16.
Приведемо
подібні члени в лівій частині нерівності і запишемо результат у вигляді 0 × х:
0 × х < –
12.
Отримана
нерівність не має рішень, оскільки при будь-якому значенні х воно звертається в числову нерівність 0 < –12, що не є вірним. Значить, не має
рішень і рівносильно йому задана нерівність.
ВІДПОВІДЬ: рішень
немає
ПРИКЛАД:
Розв'яжіть
нерівність:
7(2 – х)
≤ 3х + 44.
РОЗВ'ЯЗАННЯ:
–7х – 3х
≤ –14 +
44,
–10х ≤ 30,
х ≥ –3.
ВІДПОВІДЬ:
Нерівність
задовольняє кожне число, не менше від –3. Множини розв'язків
нерівностей зручно записувати у вигляді проміжків:
[–3; ∞),
2х – 3х < 12.
Розв'яжіть нерівність:
РОЗВ'ЯЗАННЯ:Наводимо до спільного знаменника:Наводимо подібні доданки в чисельнику:ВІДПОВІДЬ:
–5х – 23 < 0,
–5х < 23,
х
˃ –23/5.
ВІДПОВІДЬ:
Найменше ціле рішення нерівності
х = 4.
ПРИКЛАД:
–9 ≤ 3 – 2х ≤ 3,
–9 – 3 ≤ –2х ≤ 3 – 3,
–12 ≤ –2х ≤ 0,
–6 ≤ –х ≤ 0,
6 ≥ х ≥ 0,
0 ≤ х ≤ 6.
ВІДПОВІДЬ:
Безліч рішень нерівності містить наступні цілі числа:
0, 1, 2, 3, 4, 5, 6 –
всього
7 чисел.
Сукупність
нерівностей з однією змінною.
Говорять, що декілька нерівностей з однією змінною
утворюють сукупність нерівностей, якщо ставиться завдання знайти усі такі
значення змінної, кожне з яких є рішенням хоч би однієї з цих нерівностей.
Значення змінної, при якому хоч би одно з
нерівностей, що утворюють сукупність, звертається у вірну числову нерівність,
називають рішенням сукупності нерівностей.
ПРИКЛАД:
Перетворивши
кожну з нерівностей, отримаємо сукупність, рівносильну заданою:
х
<
4/11,
х
<
6/7.
За
допомогою числової прямої знаходимо, що рішенням заданої сукупності є проміжок
- Урок 1. Числові нерівності
- Урок 2. Властивості числових нерівностей
- Урок 3. Додавання і добуток числових нерівностей
- Урок 4. Числові проміжки
- Урок 6. Системи лінійних нерівностей
- Урок 7. Нелінійні нерівності
- Урок 8. Системи нелінійних нерівностей
- Урок 9. Дробово-раціональні нерівності
- Урок 10. Рішення нерівностей за допомогою графіків
- Урок 11. Нерівність з модулем
- Урок 12. Ірраціональні нерівності
- Урок 13. Нерівності з двома змінними
- Урок 14. Системи нерівностей з двома змінними
- Урок 15. Наближені обчислення
- Урок 16. Абсолютна і відносна погрішність
















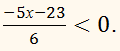



Комментариев нет:
Отправить комментарий