Урок 8. Перетворення фігур

ВІДЕО УРОК

Якщо кожну точку даної фігури змістити яким – не будь чином, то ми дістанемо нову фігуру. Говорять, що ця фігура утворилася перетворенням даної. Перетворення однієї фігури в іншу називається рухом, якщо воно зберігає відстань між точками. Поняття руху в геометрії пов’язано із звичайним уявленням про переміщення. Але якщо, говорячи про переміщення, ми уявляємо неперервний процес, то в геометрії для нас матиме значення тільки початкове і кінцеве положення фігури. Рух зберігає відстані між точками, тому переводить різні точки в різні.

Якщо кожній точці фігури  F  поставити у відповідність деяку точку площини, то всі відповідні точки утворюють деяку фігуру  F₁. Кажуть, що фігуру  F₁  одержали у результаті перетворення фігури  F. Фігуру  F₁  називають образом фігури  F.

При перетворенні фігури  F  у фігуру  F'  мають місце такі властивості:

1) кожній точці фігури  F  відповідає єдина точка фігури  F';

2) кожній точці фігури  F'  відповідає деяка точка фігури  F;

3) різним точкам фігури  F  відповідають різні точки фігури  F';

ПРИКЛАД:

Поставимо у відповідність кожній точці  Х  півкола основу перпендикуляра, опущеного з точки  Х  на діаметр – точку  Х'.

Ця відповідність буде перетворенням півкола в діаметр. Діаметр – образ півкола.

Поставимо у відповідність кожній точці кола  К  діаметрально протилежну їй точку  К'.

Ця відповідність буде перетворенням кола в коло або кола в себе. Образом кола буде те саме коло.

Переміщення.

Перетворення фігури  F, яке зберігає відстані між точками, називають переміщенням (рухом) фігури  F.

ПРИКЛАД:

Перетворенням фігури  F  у фігуру  F' – переміщення, оскільки

Властивості переміщення (руху).

1. Два рухи, виконані послідовно, дають знову рух.

2. Перетворення, обернено до даного, теж є рух.

3. Унаслідок переміщення точки, які лежать на прямій, переходять у точки, які лежать на прямій, до того ж зберігається порядок їх взаємного розташування. На рисунку

до того ж якщо точка  С  лежить між точками  А  та  В, то точка  С'  лежить між точками  А'  та  В'.
4. Унаслідок переміщення прямі переходять у прямі, промені – у промені, відрізки – у відрізки. На рисунку:

Промінь  АК – у промінь  А'К',

5. Унаслідок переміщення кут переходить у рівний йому кут. На рисунку:

6. Унаслідок переміщення паралельні прямі переходять у паралельні прямі.

Переміщення будь-яку фігуру переводить її у рівну фігуру.

Дві фігури називають рівними, якщо існує переміщення, яке переводить одну фігуру і іншу.

Симетрія.

Дві точки  Х' та  Х'  називають симетричними відносно даної точки  О, якщо точка  О – середина відрізка  ХХ'.

Точку  О вважають симетричною самій собі й називають центром симетрії.

Щоб побудувати точку  Х', симетричну до точки  Х  відносно точки  О, потрібно:

1) провести промінь  ОХ;

2) відкласти на ньому з другого боку від точки  О  відрізок 

ОХ' = ОХ.

Перетворення, за якого кожна точка  Х  фігури  F  переходить у точку  F'  фігури  Х', симетричну відносно даної точки  О, називають перетворенням симетрії відносно точки  О. фігури  F  і  F'  називають симетричними відносно точки  О.

ПРИКЛАД:

На рисунку показано побудову фігури, симетричної даній відносно точки  О.

Відрізка.

Кола.

Трикутника.

Властивості центральної симетрії.

– центральна симетрія є переміщенням, тому вона має всі властивості переміщення;

– образом прямої, що проходить через центр симетрії, є сама ця пряма, а образом прямої, яка не проходить через центр симетрії, є паралельна їй пряма.

Образом довільної точки  М(х₀; у₀)  при центральній симетрії з центром у початку координат є точка  М₁(–х₀; –у₀).

Фігуру  F  називають центральносиметричною, якщо існує така точка  О, при симетрії відносно якої фігура  F  переходить у себе.

ПРИКЛАД:

Прикладом центральносиметричної фігури є:

Квадрат.

Коло.

Центром симетрії квадрата є точка перетину його діагоналей, а кола – його центр.

Точки  Х  та  Х₁  називають симетричними відносно прямої  l, якщо пряма  l  є серединним перпендикуляром до відрізка  ХХ₁.

Осьовою симетрією відносно прямої  l  називають перетворення, при якому кожна точка  Х  фігури  F  переходить у точку  X₁  фігури  F₁, симетричну відносно прямої  l. Осьова симетрія є переміщенням (рухом), отже, вона має всі властивості переміщення. Якщо при симетрії відносно прямої  l  фігура переходить сама у себе, то фігуру називають симетричною відносно прямої  l, а пряму  l – віссю симетрії фігури. Симетрію з віссю  l  називають осьовою симетрією.

ПРИКЛАД:

На рисунках показано побудову фігури, симетричної даній відносно прямої  l.

Відрізка.

Кола.

Трикутника.

Точки, симетричні відносно осі  х, мають однакові абсциси та протилежні ординати.

Точки, симетричні відносно осі  у, мають однакові ординати та протилежні абсциси.

Поворот.

Поворотом площини навколо даної точки називається такий рух, при якому кожний промінь, що виходить з даної точки, повертається на один і той самий кут в одному і тому самому напрями. Перетворення фігур при повороті площини також називається поворотом.

Поворотом фігури  F  навколо точки  О  на кут    за годинниковою стрілкою (проти годинникової стрілки) називають перетворення фігури  F  у фігуру  F', при якому кожній точці  Х  фігури  F  ставиться у відповідність така точка  Х₁  фігури  F₁, що

ОХ' = ОХ,

∠ ХОХ' = α.

Точку  О  називають центром повороту, а кут  α – кутом повороту.

Центр повороту переходить у себе. Поворот є переміщенням (рухом).

Поворот задається:

– центром повороту;

– кутом повороту;

 – напрямом повороту.

Щоб побудувати точку  Х', у яку перейде точка  Х  унаслідок повороту навколо точки  О  на кут  α, потрібно:

1) провести промінь  ОХ;

2) від променя  ОХ  відкласти кут  ХОА, що дорівнює куту  α  на рисунку

– проти годинникової стрілки,
а на рисунку

– за годинниковою стрілкою;

3) на промені  ОА  знайти точку  Х', яка лежить на відстані  ОХ  від центру повороту  О.

Послідовне виконання двох поворотів навколо однієї й тієї ж точки є поворотом.

Щоб виконати поворот фігури  F  навколо точки  О  на кут  α, потрібно кожну точку  Х  фігури  F  змістити по дузі кола з центром  О  радіуса  ОХ  на кут  α.

Паралельне перенесення.

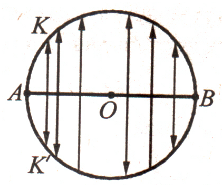
Наочно паралельне перенесення означають як перетворення, при якому точки зміщуються в одному і тому самому напрямі на одну й ту саму відстань. Таке означення має той недолік, що в ньому вживається вислів  ’’в одному і тому самому напрями’’, який сам потребує точного означення. У зв’язку з цим паралельному перенесенню ми дамо інше означення, яке відповідає тому самому наочному уявленню, але вже строге. Паралельне перенесення можна задати парою точок, указавши, яка з точок переходить у яку. Паралельне перенесення можна задати формулами.

Введемо на площині Декартові координати  х, у.

Перетворення фігури  F, при якому довільна її точка  (х; у)  переходить у точку 

(х + а; у + b),

де  а  і  b  одні й ті самі для всіх точок  (х; у), називається паралельним перенесенням.

У прямокутній системі координат паралельне перенесення, яке переводить точку  Х(х; у)  у точку  Х'(х'; у'), задається формулами:

х' = х + а;

у' = у + b,

де  а  та  b – координати вектора переносу.

Ці формули виражають координати  х_1,  у₁  точки, у яку переходить точка  (х; у)  при паралельному перенесенні.

Паралельне перенесення є рух.

Паралельним перенесенням фігури  F  називають таке перетворення фігури  F  у фігуру  F₁, при якому всі точки фігури  F  зміщуються на один і той же вектор (в одному й тому ж напрямі та на одну й ту ж відстань).

По-іншому кажуть, що всі точки фігури зміщуються уздовж паралельних прямих або прямих, які збігаються в одному й тому ж напрямі й на одну й ту ж відстань.

На рисунку

 Х Х' ∥ AA' ∥ CC' ∥ NN',

Х Х' = AA' = CC' = NN'.

Кожну точку фігури  F  змістили в одному й тому ж напрямку на одну й ту ж відстань:

Отже, фігура  F  перейде у фігуру  F'  унаслідок паралельного перенесення на вектор

Властивості:

– паралельне перенесення є переміщенням, тому має усі його властивості;

– при паралельному перенесенні точки зміщаються вздовж паралельних прямих (або прямих, які збігаються) на одну й ту саму відстань;

– при паралельному перенесенні пряма переходить у паралельну їй пряму або в себе, які б не були дві точки  А  і  А₁, існує одне і до того єдине паралельне перенесення, при якому точка  А  переходить у точку  А₁;

– переміщення, обернене до паралельного перенесення, є паралельним перенесенням;

– послідовне виконання двох паралельних перенесень є паралельним перенесенням;

– дві пів прямі називаються протилежно напрямленими, якщо кожна з них однаково напрямлена з пів прямою, доповняльною до другої;

– дві пів прямі називаються однаково напрямленими або спів напрямленими, якщо вони суміщаються паралельним перенесенням.

Тобто існує паралельне перенесення, яке переводить одну пів пряму в іншу. Якщо пів прямі  а  і  b  однаково напрямлені й пів прямі  b  і  с  однаково напрямлені, то пів прямі  а  і  с  також однаково напрямлені.

Щоб побудувати точку  А', у яку перейде точка  А  при паралельному перенесенні, що переводить точку  Х  у точку  Х', потрібно:

1) провести пряму  ХХ':

2) через точку  А  провести пряму

AA' ∥ ХХ';

3) на прямій  AA'   відкласти відрізок   

AA' = ХХ'

так, щоб промені  AA' і ХХ'  були спів напрямлені. Точка  A' – шукана.

Рівність фігур.

Дві фігури називаються рівними, якщо вони переводяться рухом одна в одну. Для позначення рівності фігур користуються звичайним знаком рівності. Запис  F = F₁  означає, фігура  F  дорівнює фігурі  F₁. У записі рівності трикутників: 

∆АВС  = ∆А₁В₁С₁ 

передбачається, що вершини, які суміщаються під час руху, стоять на відповідних місцях. За такої умови рівність трикутників, що визначається через суміщення їх рухом, і рівність, як ми її розуміли досі, виражають одне і те саме. Це означає, що коли у двох трикутниках відповідні сторони рівні і відповідні кути рівні, то ці трикутники суміщаються рухом. І навпаки, якщо два трикутники суміщаються рухом, то у них відповідні сторони рівні і відповідні кути рівні.

Перетворення подібності. 

Перетворення фігури  F  у фігуру  F’  називається перетворенням подібності, якщо при цьому перетворенні відстані між точками змінюються в одну й ту саму кількість разів.

Перетворенням подібності з коефіцієнтом  k ˃ 0  називають перетворення фігури  F  у фігуру  F₁, при якому довільним точкам  Х  та  Y  фігури  F  ставлять у відповідність такі точки  X₁  та  Y₁  фігури  F₁, що

X₁Y₁ = kXY.

Коефіцієнт  k(k ˃ 0)  називають коефіцієнтом подібності.

Це означає6 якщо довільні точки  Х  та  Y  фігури  F  унаслідок перетворення подібності переходять у точки  Х'  і  Y'  фігури  F', то

Х' Y' = kXY, де  k ˃ 0.

Переміщення є окремим випадком перетворення подібності, якщо 

k = 1.

Властивості перетворення подібності.

– перетворення подібності переводить прямі в прямі, промені – у промені, відрізки – у відрізки.

– перетворення подібності переводить кут у рівний йому кут;

– перетворення подібності переводить площини в площині.

Дві фігури називають подібними, якщо вони переводяться одна в одну перетворенням подібності. Запис  F~ F' означає: фігура   F подібна до фігури  F'. Інколи вказують коефіцієнт подібності, наприклад, якщо  k = 3, пишуть  F³~ F'. Коефіцієнт подібності    дорівнює відношенню довжин відповідних лінійних елементів фігур  F'  і  F.

Властивості подібних фігур.

– будь-яка фігура подібна сама собі: F~ F;

– якщо  F₁~ F₂, то F₂~ F₁;

– якщо  F₁~ F₂, а  F₂~ F₃, то  F₁~ F₃;

– відношення площ подібних фігур дорівнює квадрату коефіцієнта подібності, тобто якщо

F^k~ F₁.  то

Гомотетія.

Нехай даний багатокутник  ABCD.

Візьмемо довільну точку  О  і побудуємо вектори

і так далі.

Багатокутник  A₁B₁C₁D₁  буде подібним до багатокутника  ABCD.

У цій побудові використовувалася вимога, при якій точка  х  переходить в точку  Х₁  і що

точка  О  переходить в себе.

Таким чином, завдання побудови фігури, подібній цій фігурі, призводить до нового виду перетворень, яке називають гомотетією.

Гомотетією з центром  О  і коефіцієнтом  k ≠ 0  називають перетворення фігури  F  у фігуру  F',  унаслідок якого кожна точка  Х  фігури  F  переходить у точку  Х'  фігури  F'  так, що

Точку  О  називають центром гомотетії, а число  k – коефіцієнтом гомотетії. На рисунку відрізок  А₁В₁  гомотетичний відрізку  АВ  з центром гомотетії  О  і  k = 2.

Якщо при гомотетії фігура  Ф₁  переходить у фігуру  Ф₂, то ці фігури називають гомотетичними.

Якщо  k = 1, то кожна точка  Х  перейде сама в себе. Центр гомотетії переходить сам в себе.

Якщо  k ˃ 0, то гомотетичні фігури розташовуються по одну сторону від центру гомотетії. Точки  Х  і  Х₁  лежать на прямій  ОХ  по одну сторону від центру гомотетії (оскільки вектори

сонаправлени).

Якщо  k < 0, то гомотетичні фігури розташовуються по різні сторони від центру гомотетії. Точки  Х  і  Х₁  лежать на прямій  ОХ  по різні сторони від центру гомотетії (оскільки вектори

протилежно спрямовані).

Якщо  k = –1, то кожна точка  А  перейде сама в точку  А₁, для якої

Але таке перетворення – центральна симетрія. Значить, гомотетія з коефіцієнтом  –1  є центральною симетрією.

Щоб побудувати фігуру  F', гомотетичну фігуру  F, потрібно:

1) зафіксувати на площині точку  О;

2) вибрати довільну точку  Х  фігури  F;

3) відкласти на промені  ОХ  (або на доповняльному промені) відрізок  ОХ', що дорівнює  |k| ∙ ОХ;

4) провести такі побудови для кожної точки фігури  F.

Одержимо фігуру  F', яка є образом фігури  F, отриманим у результаті гомотетії.

ПРИКЛАД:

На рисунку показано побудову чотирикутника, гомотетичного чотирикутнику  АВСD  з центром гомотетії  О  і коефіцієнтом гомотетії:

а) k = 2;

б) k = –2.

Властивості гомотетії.

Гомотетія є перетворенням подібності й вона має всі властивості перетворення подібності.

Якщо при гомотетії з коефіцієнтом  k  точки  Х  і  Y  переходять в точки  X₁  і  Y₁, то

Звідси витікають наступні властивості гомотетії :

1) при гомотетії з коефіцієнтом  k  відстань між точками множиться на  |k|;

2) гомотетія всяку площину переводить в паралельну їй площину;

3) гомотетія переводити пряму в паралельну ії пряму або в саму собі, якщо дана пряма проходити через центр гомотетії :

4) на координатній площині гомотетія з центром у качану координат задається формулами

де (х; у) – координати точки  А, а  (х₁; у₁) – координати образу цієї точки при гомотетії;
5) гомотетични трикутники завжди подібні.

Завдання до уроку 8

• Завдання 1
• Завдання 2
• Завдання 3

Інші уроки:

• Урок 1. Поняття вектора
• Урок 2. Координати вектора
• Урок 3. Складання і віднімання векторів
• Урок 4. Добуток векторів
• Урок 5. Вектори в просторі
• Урок 6. Дії над векторами в просторі
• Урок 7. Рішення завдань за допомогою векторів