Два многокутника називаються подібними, якщо вони мають відповідно рівні многогранних куті і відповідно подібні грані.
Відповідні елементи подібних багатогранників називаються спорідненими. У подібних багатогранників двогранні кути рівні і однаково розташовані; відповідні ребра пропорціональні.
Якщо в піраміді провести січну площину паралельно до основи, то вона відтинає від неї другу піраміду, подібну до даної.
Подібні циліндри і конуси.
Два циліндри, конуси або зрізані конуси називаються подібними, якщо подібні їх осьові перерізи.
Об'єми подібних тіл.
Нехай Т и Т' – два простих подібних тіла. Це означає, що існує перетворення подібності, при якому тіло Т переходить у тіло Т'. Позначимо через k коефіцієнт подібності.
Об'єми двох подібних тіл відносяться як куби їх відповідних лінійних розмірів.
Квадрати об'ємів подібних тіл відносяться, як куби площ відповідних граней.
Об'єми подібних циліндрів, конусів і зрізаних конусів відносяться, як куби їх відповідних лінійних елементів (радіусів основ, висот, твірних).
Об'єми куль відносяться, як куби їх радіусів або діаметрів.
ЗАДАЧА:
Через
середину висоти піраміди проведена площина, паралельна основи. У якому відношенні
вона ділить об’єм піраміди ?
РОЗВ'ЯЗАННЯ:
Об'єм
конуса дорівнює 16. Через середину висоти паралельно
підставі конуса проведено переріз, який є підставою меншого конуса з тією самою
вершиною. Знайдіть об'єм меншого конуса.
РОЗВ'ЯЗАННЯ:
ВІДПОВІДЬ: 2
ЗАДАЧА:
У
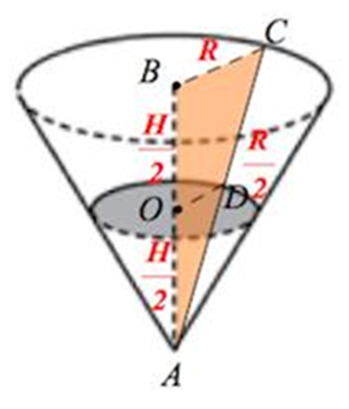
посудині, що має форму конуса, рівень рідини досягає 1/2 висоти. Об'єм рідини
дорівнює 54 мл. Скільки мілілітрів рідини
потрібно долити, щоб повністю наповнити посудину
?
РОЗВ'ЯЗАННЯ:
R/2 – радіус основи конуса, чий об'єм займає рідину, оскільки трикутники АОD і АВС подібні і коефіцієнт подібності дорівнює 2. Звідси:Об'єм конуса єЗначить долити потрібно
432 – 54 = 378 (мл).
2
спосіб
Можна
міркувати і так:
Відсічений
конус, що утворився при перетині вихідного конуса площиною паралельної основи і
перетинає висоту конуса посередині, подібний до вихідного з коефіцієнтом
подібності
1 : 2.
Отже,
обсяг вихідного конуса є 8 обсягів відсіченого конуса (обсяги подібних тіл знаходяться у відношенні
k3, де k – коефіцієнт подібності). Отже, на усічений конус припадає 7 обсягів відсіченого (малого) конуса. Тобто об'єм усіченого конуса (а значить об'єм рідини, що потрібно долити) є
7 ∙ 54 = 378.
ВІДПОВІДЬ: 378
мл
ЗАДАЧА:
У
зрізаній трикутній піраміді через сторону верхньої основи проведено площину
паралельно бічному ребру. У якому відношенні розділиться об’єм зрізаної
піраміди, якщо відповідні сторони основ пропорційні числам 1
: 3 ?
РОЗВ'ЯЗАННЯ:
A1B1ML ∥ CC1, ОО1 = Н.
Якщо
відповідні сторони основ пропорційні числам
1 : 3, то площі основ будуть пропорційні
числам 1 : 9.
S1 – площа ∆ А1В1С1,
V1
= 1/3
H (S1 + S2 + √͞͞͞͞͞S1S2)
=
=
1/3
H (S1 + 9S1 + √͞͞͞͞͞S1∙9S1) = 1/3 H (13S1).
V2 – об’єм похилої призми А1В1С1LMC:
V2
= S1 ∙ H.
V3 – об’єм фігури, що залишилася:
V3 =
V1
– V2 = 1/3
H (13S1) – S1 ∙
H =
Площі основ зрізаної піраміди S1 і S2, а її об'єм V. Визначити об'єм повної піраміди.
РОЗВ'ЯЗАННЯ:
Складаючи похідну пропорцію, дістанемо:
Враховуючи, що
V1 – V2 = V,
знаходимо:
Звідки:
ВІДПОВІДЬ:
ЗАДАЧА:
Площі основ зрізаної піраміди дорівнюють а2 і b2. Знайти площу перерізу, що паралельний до площин основ зрізаної піраміди і ділить її об'єм пополам.
РОЗВ'ЯЗАННЯ:
В зрізаній піраміді АС1 (для простоти рисунка розглядається трикутна піраміда) дано:
SАВС, SА'В'С', SA1B1C1 – подібні.
Позначимо площу шуканого перерізу А'В'С' через х2, а об'єми пірамід
SАВС, SА'В'С' і SA1B1C1
відповідно Va, Vx, Vb. Тоді:
де t – деяке число, що позначає величину цих відношень. Тоді:
Va = a3t,
Vx = x3t,
Vb = b3t.
За умовою задачі:
Va – Vx = Vx – Vb,
або
звідки:
2x3 = a3 + b3.
- Урок 1. Одиниці вимірювання об’ємові
- Урок 2. Об’єм прямий призми
- Урок 3. Об’єм похилої призми
- Урок 4. Об’єм правильної призми
- Урок 5. Об’єм прямого паралелепіпеда
- Урок 6. Об’єм похилого паралелепіпеда
- Урок 7. Об’єм прямокутного паралелепіпеда
- Урок 8. Об’єм куба
- Урок 9. Об’єм піраміди
- Урок 10. Об’єм правильної піраміди
- Урок 11. Об’єм зрізаної піраміди
- Урок 12. Об’єм циліндра
- Урок 13. Об’єм конуса
- Урок 14. Об’єм зрізаного конуса
- Урок 15. Об’єм кули та її частин
- Урок 16. Тіла обертання
- Урок 17. Комбінації тіл (2)
- Урок 18. Правильні багатогранники

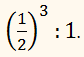




















Комментариев нет:
Отправить комментарий