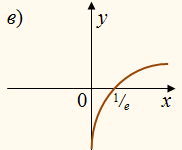Прежде чем приступить к решению примеров и задач, обязательно ознакомьтесь с теоретической частью урока
Логарифмическая функция
1. На одном из рисунков изображён график функции2. Областью определения какой из функций будет множество действительных чисел ?
а) у =
lоg3
х;
б) у =
lоg3
(–х);
в) у =
lоg3
(х2 + 1);
г) у =
lоg3
(х2 – 1).
3. Известно, что
lоg11
а < lоg11
b.
Сравните числа а и b.
а) а < b;
б) а =
b;
в) а > b;
г) сравнить невозможно.
4. Какая функция убывает на промежутку
(–∞; 1] ?
а) у =
log0,4
х;
б) у =
0,4х;
в) у =
х4;
г) у =
4/х.
5. Какая функция не будет убывающей ?
у =
lоg4
(х – 3)
с осью абсцисс.
а) (0; 4);
б) (3; 0);
в) (0; 3);
г) (4; 0).
7. Найдите
координаты точки пересечения графиков функций:
у =
lg х и
у = 3.
а) (3; 1000);
б) (1000; 3);
в) (30; 3);
г) (10; 3).
8. Областью определения какой из функций будет
множество действительных чисел ?
у =
lоg2
х ?
у =
lоg2
(х2 – 3х + 8)
с осью ординат.
а) (0; 8);
б) (3; 0);
в) (0; 3);
г) (8; 0).
11. Укажите область
определения функции.
б) (0; +∞);
в) (–∞; 4) ∪ (4; +∞);
г) (0; 4).
12. Укажите область
определения функции.
б) (–∞; +∞);
в) (–∞; –1) ∪ (–1; 0) ∪
(0; 1) ∪ (1; +∞);
г) (0; 1) ∪
(1; +∞).