Перш ніж приступити до рішення прикладів і завдань, обов'язково ознайомтеся з теоретичною частиною уроку
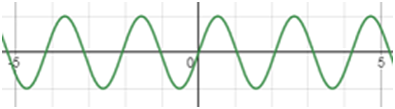
ГРАФІКИ ФУНКЦІЙ У = SIN X І Y = COS X
або
ВІДЕО УРОКОМ
1. Знайдіть координати точок перетину з осями координат графіка функції:
y = sin x.
а) (1; 0);
б) (0; 0);
в) (1; 1);
г) (0; 1).
2.
Знайдіть
координати точок перетину з осями координат графіка функції:
y = 1 + соs x.
а) (0; 1) (– π/3; 0);
б) (0; 2) (– π/3; 0);
в) (0; 1) (– π/2; 0);
г) (0; 2) (– π/2; 0).
3.
При яких значеннях х на [0; 2π) функція
у
= 2 – sin
x
приймає найбільше значення і чому воно дорівнює ?
а) у =
3 при х = 3π/2;
б) у = 1 при х = π/2;
в) у = 3 при х = π/2;
г) у = 1 при х = 3π/2.
4.
При яких значеннях х на [0; 2π) функція
у
= 3 + соs
x
приймає найменше значення і чому воно одно ?
а) у =
4 при х = 2π;
б) у = 2 при х = 2π;
в) у = 4 при х = π;
г) у = 2 при х = π.
5. Які
значення х, для яких f(x) = 0 ?
а) π/2
+ 2πn, n ∈
Z;
б) π/4 + πn,
n ∈ Z;
в) π/2 + πn,
n ∈ Z;
г) π/4 + 2πn,
n ∈ Z.
6.
Які значення х, для яких f(x) < 0 ?
а) π/4 +
2πn < x < 3π/4
+ πn, n ∈ Z;
б) π/2 + 2πn
< x < 3π/4 + πn, n ∈
Z;
в) π/2 + πn
< x < 3π/4 + πn, n ∈
Z;
г) π/4 + πn
< x < 3π/4 + πn, n ∈
Z.
7.
Які значення х, для яких f(x) ˃ 0 ?
а) –π/4
+ πn < x < π/4 + πn, n ∈
Z;
б) –π/4 + 2πn
< x < π/4 + πn,
n ∈ Z;
в) –π/4 + 2πn
< x < π/4 + 2πn,
n ∈ Z;
г) –π/4 + πn
< x < π/4 + 2πn,
n ∈ Z.
8. Які
проміжки зростання функції ?
а) [–π/2
+ 2πn; 2πn], n ∈ Z;
б) [–π/2 + πn;
2πn], n ∈
Z;
в) [–π/2 + πn;
πn], n ∈
Z;
г) [–π/2 + 2πn;
πn], n ∈
Z.
9. Які
проміжки зменшення функції ?
а) [πn;
π/2
+
πn], n ∈
Z;
б) [2πn; π/2
+
πn], n ∈
Z;
в) [2πn; π/2
+
2πn], n ∈
Z;
г) [πn; π/2
+
2πn], n ∈
Z.
10. Вкажіть значення
х,
за яких функція має максимум.
а) π/2 n, n ∈
Z;
б) π/4 n,
n ∈ Z;
в) πn, n ∈ Z;
г) 2πn, n ∈ Z.
11. Вкажіть значення
х,
за яких функція має мінімум.
а) π/2 + 2πn, n ∈ Z;
б) π/2
+
πn, n ∈
Z;
в) π/4
+
πn, n ∈
Z;
г) π/4
+
2πn, n ∈
Z.
12. Чи оборотна функція на R ?
а) ;
б) оборотна;
в) ;