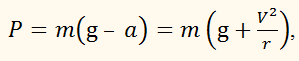ВИДЕО УРОК
Силу тяжіння, як і
всяку іншу силу, можна вимірювати динамометрами. Динамометри, спеціально
призначені для виміру сили тяжіння, називають пружинними вагами, тому що з їх
допомогою можна виміряти вагу тіла. Що це за величина – вага ?
ДОСВІД:
Розглянемо процес деформації пружини динамометра, коли до неї підвішений деякий вантаж. Звернемо увагу не лише на те, що відбувається з пружиною, але і на те, що відбувається з самим вантажем, підвішеним до пружини.
зображена пружина динамометра до того, як до неї був підвішений вантаж. Це недеформована пружина (масою пружини нехтуємо).
Підвісимо до пружини вантаж. При своєму падінні він захоплює за собою і нижній кінець пружини, внаслідок чого пружина деформується, як це показано на малюнку.
Сила пружності, що виникає при цьому теж прикладена до тіла, але спрямована вгору. При певному значенні подовження пружини сила пружності по абсолютному значенню стає рівній силі тяжіння Під дією цих двох сил, рівнодійна яких дорівнює нулю, вантаж встановлюється в стані спокою.
Але якщо пружина динамометра діє на вантаж, то за третім законом Ньютона і вантаж діє на пружину з такою ж по абсолютному значенню силою, але спрямованою в протилежну сторону, тобто вниз. Це теж сила пружності. Виникає вона через те, що і вантаж (а не тільки пружина) деформується. У сильно збільшеному виді ця деформація (подовження) показана на малюнку Ось цю силу, прикладену не до тіла, а до пружини, і називають вагою тіла. Вагу тіла прийнято означати буквою Р.
Якщо тіло не підвішувати, а помістити на горизонтальну опору, те воно і на опору діє з силою, що теж називається вагою.
Вагою тіла називається сила, з якою нерухоме відносно Землі тіло давить на горизонтальну підставку, на якій воно лежить, або розтягує нитку, на якій воно висить.
Вага тіла приблизно дорівнює силі тяжіння тіла Землею. Згідно з другим законом Ньютона, вага тіла
P = mg.
Вага тіла в системі СІ вимірюється тими ж одиницями, що і сила – ньютонами. На практиці часто користуються одиницею сили (ваги)
1 кГ.
1
кГ
– це сила, що повідомляє масі 1 кг прискорення
g
= 9,80665 м/сек2.
Очевидно,
1 кГ = 1 кг × 9,80665 м/сек2
≈ 9,8 н = 9,8 × 105 дин.
Вага тіла – це сила, прикладена не до тіла, а до опори або підвісу.
Не обов'язково, щоб
опора або підвіс були спіральною пружиною. Тіло можна підвісити на нитці, на
дроті або помістити на стіл. На нитку, дріт або стіл діятиме вага тіла.
У розглянутих прикладах
вага тіла, очевидно дорівнює силі тяжіння. Але це вірно тільки тоді, коли опора
або підвіс знаходяться у спокої відносно Землі (чи рухаються прямолінійно і
рівномірно).
Вага і сила тяжіння не одно і те ж: вага і сила тяжіння завжди прикладені до різних тіл.
Вимір маси тіл зважуванням.
Масу тіла можна визначити, вимірюючи відношення прискорень при взаємодії цього тіла з тілом, прийнятим за еталон маси. Цей спосіб дуже незручний і на практиці зазвичай не застосовується. Розглянемо інший, зручніший спосіб виміру маси. Цей спосіб називають зважуванням. Визначення маси методом зважування ґрунтоване на тому, що сила тяжіння, що діє на тіло, і маса цього тіла пропорційні один одному:
А силу тяжіння можна вимірювати на вагах, оскільки вона по абсолютному значенню дорівнює вазі тіла, якщо ваги разом із зважуваним тілом покояться відносно Землі. Тому, вимірявши вагу тіла пружинними вагами і знаючи прискорення вільного падіння у місці, де робиться зважування, можна вичислити масу по формулі: Ще зручніше визначати масу зважуванням на важільних вагах. На важільних вагах порівнюють ваги тіл і гир. Коли ваги урівноважені, можна стверджувати, що вага тіла дорівнює вазі гир. Але якщо рівні ваги тіл, то рівні їх маси. Оскільки на гирях (важках) вказані саме їх маси, то масу тіла ми визначаємо, просто склавши числа, вказані на важках.
Важільні ваги дуже
чутливий прилад. Найменша маса, яку можна виміряти найбільш чутливими вагами,
складає декілька мільйонних доль грама.
Вага тіла, що рухається з прискоренням.
Ми знаємо, що вага тіла – це сила, з якою тіло діє на опору або на підвіс. Якщо опора або підвіс покояться відносно Землі або рухаються відносно неї прямолінійно і рівномірно, то вага тіла дорівнює силі тяжіння
Але вага тіла може істотно відрізнятися від значення сили тяжіння, якщо опора або підвіс рухаються з прискоренням вгору або вниз. Чому ?
Подивимося, що покажуть
пружинні ваги, якщо вони разом з підвішеним до них тілам рухаються з
прискоренням вгору або вниз.
ДОСВІД:
Підвісимо до пружинних вагів який-небудь вантаж і дамо їм можливість рухатися з деяким прискоренням
Для цього можна узяти ваги з вантажем в руку і різко відпустимо їх вниз, повідомивши їм прискорення, спрямоване вниз. Ми побачимо, що під час опускання вагів їх стрільця переміщається вгору. Це означає, що вага вантажу під час опускання стала менше, ніж він був у разі вагів, що покояться. Якщо, навпаки, різко підняти ваги, стрілка опуститься, показуючи, що вага вантажу збільшується. Чим пояснюється це зменшення або збільшення ваги при прискореному русі динамометра з вантажем ?
Відповідь на це дає другий закон Ньютона. Подивимося, які сили діють на вантаж. На нього діють сила тяжіння спрямована вниз, і сила пружності пружини вагів, спрямована вгору. Під дією цих двох сил тіло і рухається з прискоренням яке може бути спрямоване як вниз, так і вгору залежно від того, чи будемо ми опускати ваги або піднімати їх.
За другим законом Ньютона Звідси З такою ж по модулю силою, але спрямованою протилежно силі вантаж діє на пружину. А ця сила і є вага вантажу Отже, Вектори паралельні вертикальною примою. Направивши координатну вісь Х по вертикалі вниз, можна формулу
написати у формі
алгебри для проекцій цих векторів на вертикальну вісь:
P = m(g – a).
P = m(g – a)
cледует, що P <
mg.
Вага тіла,
напрям прискорення якого співпадає з напрямом прискорення вільного падіння,
менше ваги тіла, що покоїться.
P = m(g – a)
P ˃ mg.
Вага зменшується або
збільшується не лише тоді, коли тіло підвішене до пружинних вагів. Те ж саме
відноситься і до будь-якого підвісу, і до будь-якої опори.
ПРИКЛАД:
Направимо координатну вісь Х вертикально вниз. Тоді за другим законом Ньютона звідки Вага автомобіля (сила, з якою він давить на міст) за третім законом Ньютона рівна – Отже, P < mg.
Точно
також зменшується і вага пасажирів, що їдуть в автомобілі по опуклому мосту.
Зменшення ваги тим більше, чим більше швидкості автомобіля.
ПРИКЛАД:
𝜔2R ≈ 8,6
∙ 10-4 м/сек2,
те
при грубих розрахунках величиною 𝜔2R
зазвичай нехтують і вважають, що і на
екваторі вага тіла рівна mg.
ПРИКЛАД:
Таким чином, вага льотчика більше
<<нормальної>> ваги, рівної силі тяжіння mg, на величину
Якщо при виході з
пікірування доцентрове прискорення
перевищує по абсолютному
значенню прискорення вільного падіння
в g і n разів
те
вага льотчика
P = m(g + ng) =
mg(n + 1),
тобто
він буде в n + 1 раз більше <<нормальної>> ваги
льотчика.
При перевантаженні збільшують свою вагу і
внутрішні органи льотчика, збільшується сила, з якою вони діють один на одного
і на його остов (скелет). Це викликає хворобливі відчуття, а при
надмірному перевантаженні може стати небезпечним для здоров'я. Треновані пілоти
витримують перевантаження до 10 mg ( зазвичай перевантаження виражають не через величину mg, а через величину g і
говорять, що перевантаження рівне, наприклад, 10 g).