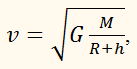ВИДЕО УРОК
Невагомість.
Розглянемо випадок, коли вантаж разом з вагами вільно падає, тобто коли ваги просто випускають з рук.
Досвід показує, що під час вільного падіння стрілка вагів встановлюється на нулі: вага виявляється рівним нулю. І це зрозуміло. Адже коли тягар падає під дією тяжіння до Землі, пружина терезів << сама слід за ним >>.
Тому вона не деформується. Але якщо пружина не деформується, то на прикріплений до неї вантаж ніяка сила з її боку не діє. Вантаж тому теж не деформований і теж не діє на пружину. Вантаж став невагомим.
Те, що при вільному падінні вага тіла дорівнює нулю,
прямо випливає з формули:
P = m(g – a).
При вільному падінні тіла a = g. Отже,
P = m(g – g) = 0.
При цьому умови опора з тілом не взаємодіє.
Причина невагомості полягає в тому, що сила всесвітнього тяжіння повідомляє тілу і його опорі однакові прискорення. Тому будь-яке тіло, яке рухається тільки під дією сил всесвітнього тяжіння, знаходиться в стані невагомості.
Саме в таких умовах і знаходиться вільно падаюче тіло.
Цей факт ілюструється наступним досвідом.
ДОСВІД:
На штативі укріплений блок, через який перекинута нитка.
На кінці цієї нитки підвішена чашка з двома вантажами досить великої маси. Верхній вантаж щільно прилягає до нижнього. Інший кінець нитки прикріплений до штатива. Між вантажами поміщена смужка тонкого паперу. Вільний кінець її тримають нерухомо в руці. Якщо вантаж опускати повільно, то папір, розтягуючись, розірветься, тому що на затиснутий кінець смужки діє сила тертя спокою. Тепер замінимо смужку паперу нової і повторимо досвід таким чином, щоб вантаж вільно падав. При падінні вантажу смужка паперу залишиться в руках нерозірваної. Значить, при падінні вантажі не тиснули один на одного, і сила тертя спокою дорівнювала нулю. Це і доводить, що вантажі при вільному падінні перебувають в стані невагомості.
Штучні супутники Землі. Перша космічна швидкість.
При русі тіла на висоті h над Землею зі швидкістю
в горизонтальному напрямку, тобто паралельно поверхні Землі, воно описує особливу траєкторію – параболу, рухаючись по якій воно падає на Землю. При розгляді такого руху тіла ми вважали, що поверхня Землі плоска. Таке спрощення справедливо при порівняно невеликих швидкостях
при яких переміщення тіла в горизонтальному напрямку невеликі.
Але в дійсності Земля – це куля. Тому одночасно з просуванням тіла по своїй траєкторії поверхню Землі кілька віддаляється від нього. Можна підібрати таке значення швидкості тіла при якому поверхня Землі через її кривизни буде віддалятися від тіла як раз на стільки, на скільки тіло наближається до Землі завдяки тяжінню до неї. Тоді тіло буде рухатися на постійній відстані h від поверхні Землі, тобто по колу радіусом
R + h,
Яка ця швидкість ? Раз тіло рухається рівномірно по колу, то його прискорення за абсолютною величиною дорівнює:
Це прискорення тілу повідомляє сила тяжіння Землі:
(тут М – маса Землі, m – маса тіла). За другим законом Ньютона звідки,
Супутником Землі може стати тіло будь-якої маси, аби
йому була повідомлена достатня швидкість. Обчислимо цю швидкість для супутника,
що запускається поблизу поверхні Землі (h = 0).
В цьому випадкуНагадаємо, що
отже,
Звідси Підставивши в цю формулу значення величини і
R = 6,4 ∙ 106 м,
отримуємо:
Таку швидкість в горизонтальному напрямку потрібно повідомити тілу біля поверхні Землі, щоб воно не впало, а стало її супутником, що рухається по круговій орбіті. Цю швидкість називають першою космічною швидкістю.
Вісім кілометрів в секунду – це майже 29 тисяч кілометрів на годину. Повідомити таку величезну швидкість тіла, не просто. І тільки в 1957 р радянським ученим вперше в історії людства вдалося за допомогою потужної ракети повідомити першу космічну швидкість тіла масою близько 84 кг. Це тіло і стало першим штучним супутником Землі.
Рух супутників навколо Землі відбувається під дією
тільки однієї сили – сили всесвітнього тяжіння, що повідомляє супутнику і усіх
предметів, що знаходяться в ньому, однакові прискорення. В такому випадку
втрачає сенс поняття ваги. Адже в цьому випадку будь-яке тіло і його <<
опора >> один одного не деформують і не можуть << тиснути >>
друг на друга. Це означає, що всі тіла в супутнику, в тому числі і пасажири,
перебувають в стані невагомості.
Рух на поворотах.
Для того щоб тіло рухалося по колу, необхідно, щоб сила, прикладена до нього, була направлена до центру кола. Якщо на тіло діє кілька сил, то до центру кола повинна бути спрямована рівнодіюча цих сил.
ПРИКЛАД:
Розглянемо рух залізничного вигону на заокругленні горизонтального шляху.
Поки потяг рухається по прямолінійній ділянці шляху з постійною швидкістю
на будь-який вагон, звичайно, діє сила тяжіння, але вона врівноважується спрямованої вгору силою пружності (реакції) рейок. Що ж стосується сили тертя, то вона врівноважується силою, що діє з боку локомотива. Але ось вагон дійшов до закруглення колії. У цьому місці він поверне і почне рухатися по дузі кола. Яка ж сила змушує вагон змінювати напрямок його швидкості, тобто рухатися з прискоренням ? Цією силою є сила пружності (сила реакції), що діє на колеса вагона з боку рейки.
Колеса залізничних вагонів мають так звану реборду, що стикається з рейками не зверху, а збоку.
Поки вагон рухається по прямолінійній ділянці шляху, реборда особливої ролі не грає і деформується лише та частина колеса, яка прилягає до рейки зверху. Пройшовши точку А,
колесо, продовжуючи свій рух в колишньому напрямі, діє на рейок ребордою і деформує його збоку - рейок вигинається назовні (деформується, звичайно, і сама реборда). При цьому виникає сила пружності спрямована перпендикулярно бічній поверхні рейки. Ця сила і змушує вагон рухатися по колу. Якби колеса вагону не мали реборду, така сила не могла б виникнути і вагон неодмінно зійшов би з рейок.
Прискорення вагона, що рухається зі швидкістю по заокругленню радіусом r, так само по абсолютній величині Тому сила пружності діюча на реборди з боку деформованого рейки (а значить, і на вагон) і викликає це прискорення, за другим законом Ньютона повинна бути дорівнює по абсолютній величині де m – маса вагона.
Деформація рейки досягає якраз такої величини, при якій сила пружності, викликана цієї деформацією, повідомляє вагону прискорення Деформація ця дуже мала і на око непомітна (білий пунктир на малюнку). Для зменшення зносу рейок і реборд необхідно зменшити силу тертя між ними, тобто зменшити силу тиску рейки на реборди. Для цього полотно залізниці на заокругленні роблять злегка похилим у бік центру заокруглення. В цьому випадку сила реакції рейок (сила пружності) НЕ врівноважує силу тяжіння їх рівнодіюча направлена приблизно до центру повороту. Це, звичайно, << полегшує >> в тому сенсі, що зменшується сила пружності що діє з боку рейки на реборди. Дійсно, тепер той же доцентровий прискорення вагону повідомляють дві сили: тому при малому куті нахилу можна написати: звідки Звідси видно, що модуль сили, що діє на реборди, тепер став менше на величину Тому меншим буде знос рейки і реборди.
У автомобіля немає реборди. При русі автомобіля на поворотах шосе доцентровий прискорення йому повідомляє сила сухого тертя між шинами і асфальтовим покриттям.