Урок 15. Рациональные числа

суббота, 27 сентября 2014 г.

Урок 15. Рациональные числа

Положительные и отрицательные рациональные числа.

Положительные числа (целые и дроби), отрицательные числа (целые и дроби) и число 0 называются рациональными числами.

Любое положительное рациональное число больше чем отрицательное число и больше нуля.

Для определения температуры воздуха используют понятие положительных и отрицательных рациональных чисел. Температура выше нуля обозначается положительными числами. Температура ниже нуля обозначается отрицательными числами.

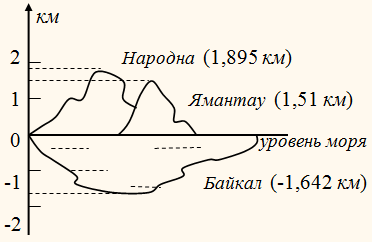
Отрицательные рациональны числа обозначают не только температуру. Ими, например, можно задавать положение некоторого места земной поверхности относительно уровня моря.

Координатная прямая.

Рациональные числа удобно изображать на координатной прямой. Каждому рациональному числу на координатной прямой будет соответствовать определённая точка и причём единственная.

Двум рациональным числам, которые отличаются только знаками, на числовой оси соответствуют точки, расположенные по обе стороны от нулевой точки и на одинаковых расстояниях от неё. Такие пары чисел называют противоположными числами.

ПРИМЕР:

Число 9,3 противоположно числу –9,3, и наоборот.

Противоположными называют также знаки + и – .

Абсолютная величина рациональных чисел.

Два противоположных числа, например +7,5 и –7,5, отличаются знаками, но записываются одинаковыми цифрами. Говорят, что они имеют одинаковые абсолютные величины. Абсолютная величина каждого из них равна 7,5.

Абсолютной величиной положительного числа называется само это число, абсолютной величиной отрицательного числа называется противоположное ему число, абсолютной величиной числа 0 называется само число 0.

Вместо термина абсолютная величина числа употребляют – модуль числа.

Для обозначения модуля числа используют две вертикальные чёрточки:

|а| (читают: модуль числа а, или модуль а).

ПРИМЕР:

|15,3| = 15,3,

|–20,1| = 20,1,

|0| = 0.

Модулем положительного числа и числа 0 есть само число.

Модулем отрицательного числа есть противоположное ему число.

Модули противоположных чисел равны, поскольку расстояние от нуля до точек с противоположными координатами равны.

ПРИМЕР:

|–2,2| = 2,2,

|2,2| = 2,2.

ПРИМЕР:

|х| = –3,7

неправильно при всех х, так как модуль любого числа всегда положительное число или нуль.

Расстояние от начала отсчёта до точки, что изображает число на координатной прямой, называется модулем этого числа.

Сравнение рациональных чисел.

Отрицательные рациональные числа сравнивают как между собой, так и с положительными рациональными числами.

Из двух рациональных чисел меньшим будет то, изображение которого на координатной прямой находится левее, а большим – то, изображение которого находится правее.

Отсюда вытекают следующие положения:

– всякое положительное рациональное число больше нуля и больше отрицательного числа;

– всякое отрицательное рациональное число меньше нуля;

– из двух отрицательных рациональных чисел больше то, у которого модуль меньше;

ПРИМЕР:

3,2 > 0;

1,1 > –5;

–3,5 > –10;

–3,6 < 0;

–4 < –1,5;

Равными считаются только те числа, у которых и знаки, и модули равны.

ПРИМЕР:

–3,2 = –3,2;

5,2 = 5,2.

Задания к уроку 15

Другие уроки:

Уроки математики и физики для школьников и родителей

суббота, 27 сентября 2014 г.