ВИДЕО УРОК
Общим кратным
данных чисел называется натуральное число, которое делится на каждое из
данных чисел (без остатка).
ПРИМЕР:
Числа 12, 24 и 36 являются общими кратными чисел 3 и 4.
Наименьшее общее кратное.
Из всех общих
кратных особый интерес представляет наименьшее общее кратное (НОК).
Наименьшим общим
кратным нескольких чисел называется самое меньшее натуральное число, которое
делится на каждое из данных чисел.
Наименьшее общее кратное (НОК) чисел а и b
– это наименьшее число, которое кратно а и b.
Другими словами, это такое маленькое число, которое делится без остатка на
число а и число
b.
Определение
содержит две переменные а и b. Подставим вместо этих переменных любые два числа.
Например, вместо переменной а подставим число 9, а вместо переменной
b подставим
число 12. Прочитаем определение:
Наименьшее общее
кратное чисел 9 и 12 – это
наименьшее число, которое кратно 9 и 12.
Другими словами, это такое маленькое число, которое делится без остатка на
число 9 и число 12.
Из определения понятно,
что наименьшее общее кратное это наименьшее число, которое делится без остатка
на 9 и 12. Это наименьшее общее кратное нужно найти.ПРИМЕР:
Для чисел 10 и 15 наименьшим общим кратным (сокращенно НОК)
будет число 30
НОК (10, 15) = 30;
Для чисел 12 и 18 таковым будет число 36
НОК (12, 18) = 36;
Для чисел 6,
15 и 20 –
очевидно, число 60,
так как никакое натуральное число, меньшее
60, не делится на 6,
на 15 и на 20,
а 60 делится на эти числа.
НОК (6, 15, 20)
= 60.
Получим следующий результат:
Теперь найдём общие кратные обоих чисел. Найдя, сразу подчеркнём их:
Общим кратным для чисел 9 и 12 являются кратные 36 и 72. Наименьшим же из них является 36. Значит наименьшее общее кратное для чисел 9 и 12 это число 36. Данное число делится на 9 и 12 без остатка:
Для нахождения
наименьшего общего кратного (НОК)
можно пользоваться тремя способами.
Первый способ нахождения НОК.
Первый способ
заключается в том, что можно выписать первые кратные двух чисел, а затем
выбрать среди этих кратных такое число, которое будет общим для обоих чисел и
маленьким.
ПРИМЕР:
Найти НОК чисел 9 и 12.
РЕШЕНИЕ:
В первую очередь, найдём первые кратные для числа 9.
Чтобы найти кратные для 9, нужно эту девятку поочерёдно умножить на числа от 1 до 9. Получаемые ответы будут кратными для числа 9.
9 × 1 = 9
9 × 2 = 18
9 × 3 = 27
9 × 4 = 36
9 × 5 = 45
9 × 6 = 54
9 × 7 = 63
9 × 8 = 72
9 × 9 = 81
Теперь находим кратные для числа 12.
Для этого поочерёдно умножим число 12 на все числа
от 1 до 12.
12 × 1 = 12
12 × 2 = 24
12 × 3 = 36
12 × 4 = 48
12 × 5 = 60
12 × 6 = 72
12 × 7 = 84
12 × 8 = 96
12 × 9 = 108
12 × 10 = 120
12 × 11 = 132
12 × 12 = 144
Получим следующий результат:
Теперь найдём общие кратные обоих чисел. Найдя, сразу подчеркнём их:
Общим кратным для чисел 9 и 12 являются кратные 36 и 72. Наименьшим же из них является 36. Значит наименьшее общее кратное для чисел 9 и 12 это число 36. Данное число делится на 9 и 12 без остатка:
36 : 9 = 4,
36 : 12 = 3.
ОТВЕТ:
НОК (9; 12) = 36
Второй способ нахождения НОК.
Второй способ
заключается в том, что числа, для которых ищется наименьшее общее кратное,
раскладываются на простые множители. Затем выписываются множители, входящие в
первое разложение, и добавляются недостающие
множители из второго разложения. Полученные множители перемножают и
получают НОК.
Чтобы найти наименьшее общее кратное нескольких
чисел, надо разложить эти числа на простые множители, затем, взяв разложение
одного из них, умножить его на недостающие простые множители из разложений
других чисел.
ПРИМЕР:
Найти НОК чисел 9 и 12.
РЕШЕНИЕ:
Разложим на множители число 9.
Разложим на множители
число 12.
Выпишем первое разложение
3 × 3
Теперь допишем множители из второго разложения, которых
нет в первом разложении. В первом разложении нет двух двоек. Их и допишем:
3 × 3 × 2 × 2.
Перемножим эти множители:
3 × 3 × 2 × 2 = 36.
Получили ответ 36. Значит наименьшее общее кратное чисел 9 и 12 это число 36.
Данное число делится на 9 и 12
без остатка:
36 : 9 = 4,
36 : 12 = 3.
ОТВЕТ:
НОК (9; 12) = 36
Всё сводится к
тому, чтобы организовать новое разложение, куда входят оба разложения сразу.
Разложением первого
числа 9 являлись
множители 3 и 3, а разложением второго числа 12 являлись
множители 2,
2 и 3.
Задача состояла в
том, чтобы организовать новое разложение, куда входило бы разложение числа 9 и разложение
числа 12 одновременно. Для
этого мы выписали разложение первого числа и дописали туда множители из второго
разложения, которых не было в первом разложении. В результате получилось новое
разложение
3 × 3 × 2 × 2.
Видно, что в него
одновременно входят разложение числа 9 и разложение числа 12.
ПРИМЕР:
Пусть требуется найти наименьшее общее кратное чисел 90, 60 и 50.
Разложим предварительно эти числа на простые множители:
90 = 2 × 3 × 3 × 5;
60 = 2 × 2 × 3 × 5;
50 = 2 × 5 × 5.
Наименьшее общее кратное должно делиться на 90,
значит, в состав его должны входить все множители числа 90. Далее наименьшее кратное должно делиться и на 60,
т.е. в его состав должны входить множители и этого числа, наконец, одновременно
с этим оно должно делиться и на последнее число – 50,
следовательно, оно должно содержать множители и этого последнего числа.
Учитывая все эти обстоятельства, поступим так: выпишем сначала
все множители первого числа (90),
а затем, что бы обеспечить делимость искомого кратного на остальные числа,
добавим к написанным множителям из других чисел те множители, которых недостает
в разложении числа 90.
Получим следующее:
НОК (90, 60, 50) =
2 × 3 × 3 × 5 × 2 × 5 = 900.
ПРИМЕР:
Найти наименьшее общее кратное двух чисел
А = 180 и
В = 140.
РЕШЕНИЕ:
А = 2 × 90 = 2 × 2 × 45 =
2 × 2 × 3 × 15 =
2 × 2 × 3 × 3 × 5;
В = 2 × 70 = 2 × 2 × 35 =
2 × 2 × 5 × 7.
Вычисляем С, равное наименьшему общему кратному чисел А и В.
С = 2 × 2 × 3 × 3 × 5 ×
7= 1260.
ОТВЕТ: 1260
ПРИМЕР:
Найти НОК чисел 50 и 180.
РЕШЕНИЕ:
Разложим на множители число 50.
Разложим на множители
число 180.
Выпишем первое разложение:
2 × 5 × 5.
Теперь допишем множители из
второго разложения, которых нет в первом разложении. В первом разложении нет
ещё одной двойки и двух троек. Их и допишем:
2 × 5 × 5 × 2 × 3 × 3.
Теперь перемножим эти множители:
2 × 5 × 5 × 2 × 3 × 3 = 900.
Получили ответ 900. Значит наименьшее общее кратное чисел 50 и 180 это число 900.
Данное число делится на 50 и 180
без остатка:
900 : 50 = 18,
900 : 180 = 5.
ОТВЕТ:
НОК (50; 180) = 900
ПРИМЕР:
Найти НОК чисел 8, 15 и 33.
РЕШЕНИЕ:
Разложим на множители число 8.
Разложим на множители
число 15.
Разложим на множители
число 33.
Выпишем первое разложение:
2 × 2 × 2.
Теперь допишем множители из
второго и третьего разложения, которых нет в первом разложении. Допишем
множители 3 и 5 из второго
разложения, и множитель 11 из третьего
разложения:
2 × 2 × 2 × 3 × 5 × 11.
Теперь перемножим эти множители:
2 × 2 × 2 × 3 × 5 × 11 = 1320.
Получили ответ 1320. Значит наименьшее общее кратное чисел 8,
15 и 33 это число
1320.
Данное число делится на 8, 15 и 33
без остатка:
1320 : 8 = 165,
1320 : 15 = 88,
1320 : 33 = 40.
ОТВЕТ:
НОК (8; 15; 33) = 1320
Если какой-то простой множитель входит в эти разложения в разных степенях,
то в наименьшее общее кратное он входит в наибольшей из этих степеней.
ПРИМЕР:
Найти НОК чисел 72 и 108.
Разложим данные числа на множители:
72 = 23 × 32,
108 = 22
× 33.
Выпишем все множители числа 108 (это удобнее, так как число 108 больше
72) и, добавив множитель 2,
который ещё дополнительно имеется в числе
72, получим
НОК (72, 108) =
23 × 33
= 216.
Если большее из
данных чисел делится на все остальные, то оно и будет наименьшим общим кратным
этих чисел.
ПРИМЕР:
НОК (60, 120, 40) =
120.
Если никакая пара
данных чисел не имеет общих множителей отличных от единицы, то для нахождения
наименьшего общего кратного данных чисел их нужно перемножить.
ПРИМЕР:
Наименьшее общее кратное чисел
7, 8, и 11
равно их произведению, т. е.
НОК (7, 8, 11) =
7 × 8 × 11 = 616.
Третий способ нахождения НОК.
Им можно пользоваться, если его ищут для двух чисел, и при условии, что уже
найден наибольший общий делитель этих чисел.
Известно, чтоНаименьшее общее кратное двух чисел равно произведению этих чисел, деленному на их наибольший общий делитель.
ПРИМЕР:
Найти НОК чисел
360 и 70.
Так как
НОД (360, 70) = 10,
то
НОК (360, 70) =
360 × 70 : 10 =
2520.
Данный способ разумнее использовать, когда одновременно нужно найти НОД и НОК двух чисел.
ПРИМЕР:
Найти НОД и НОК чисел 24 и 12.
РЕШЕНИЕ:
Сначала найдём НОД этих
чисел:
Теперь для нахождения наименьшего общего кратного
чисел 24 и 12, нужно перемножить эти два числа и полученный результат
разделить на их наибольший общий делитель.
Сначала перемножим числа 24 и 12:
Разделим полученное число
288 на НОД чисел 24 и 12:
288 : 12 = 24.
Получили ответ 24. Значит наименьшее общее кратное чисел 24 и 12 равно 24.
ОТВЕТ:
НОК (24; 12) = 24
ПРИМЕР:
Найти НОД и НОК чисел 36 и 48.
РЕШЕНИЕ:
Сначала найдём НОД этих
чисел:
Теперь для нахождения наименьшего общего кратного
чисел 36 и 48, нужно перемножить эти два числа и полученный результат
разделить на их наибольший общий делитель.
Сначала перемножим числа 36 и 48:
Разделим полученное
число 1728 на НОД
чисел 36 и 48:
Получили ответ 144. Значит наименьшее общее кратное чисел 36 и 48 равно 144.
ОТВЕТ:
НОК (36; 48) = 144
Для проверки можно
найти НОК обычным
вторым способом, которым мы пользовались ранее. Если всё сделано правильно, то
мы должны получить ответ 144.
Чтобы найти этим способом наименьшее общее
кратное трёх и более чисел, сначала находят наименьшее общее кратное
каких-нибудь двух из них, потом – наименьшее общее кратное этого наименьшего
кратного и какого-нибудь третьего данного числа и так далее.
ДРУГИЕ УРОКИ
- Урок 1. Нумерация
- Урок 2. Сложение натуральных чисел
- Урок 3. Вычитание натуральных чисел
- Урок 4. Таблица умножения
- Урок 5. Умножение натуральных чисел
- Урок 6. Деление натуральных чисел
- Урок 7. Степень числа
- Урок 8. Измерение величины
- Урок 9. Деление с остатком
- Урок 10. Делимость натуральных чисел
- Урок 11. Наибольший общий делитель (НОД)
- Урок 13. Обыкновенные дроби
- Урок 14. Преобразование дробей
- Урок 15. Сложение дробей
- Урок 16. Вычитание дробей
- Урок 17. Умножение дробей
- Урок 18. Деление дробей
- Урок 19. Нахождение дроби от числа (задачи)
- Урок 20. Нахождение числа по известной его части (задачи)
- Урок 21. Конечные десятичные дроби
- Урок 22. Сложение десятичных дробей
- Урок 23. Вычитание десятичных дробей
- Урок 24. Умножение десятичных дробей
- Урок 25. Деление десятичных дробей
- Урок 26. Округление чисел











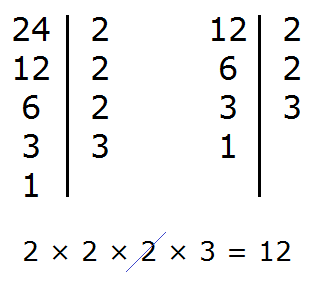





Комментариев нет:
Отправить комментарий