понедельник, 19 октября 2015 г.

Урок 24. Віднімання алгебраїчних дробів

Ви знаєте правило забирання звичайних дробів з однаковими знаменниками. Це правило можна виразити такою рівністю:

За таким самим правилом віднімають алгебраїчні дроби з однаковим знаменником.

Віднімання дробів з однаковими знаменниками.

Різниця двох (і взагалі будь-якого кінцевого числа) алгебраїчних дробів з однаковими знаменниками тотожно дорівнює дробу з тим же знаменником і з чисельником, рівним різниці чисельників дробів, що складаються:
Щоб знайти різницю дробів з однаковими знаменниками, треба від чисельника зменшуваного відняти чисельник від’ємника, а знаменник залишити той самий.

ПРИКЛАД:

 Складемо дроби:

РОЗВ'ЯЗАННЯ:
Знаменники дробів є протилежними виразами. Змінимо знаки в знаменнику другого дробу і перед цим дробом. Отримаємо:
Тепер можна застосовувати правило віднімання дробів з однаковими знаменниками:

Віднімання дробів з однаковими знаменниками.

Використовуючи основну властивість дробу, можна віднімання дробу з різними знаменниками привести до віднімання з однаковими знаменниками. Нехай потрібно відняти два дроби алгебри:

Можна записати

Тоді

Тут  за спільний знаменник вибрано вираження, яке дорівнює твору знаменнику цих дробів. Відмітимо, що твір знаменників цих дробів не завжди буде найбільшим загальним дільником знаменника. Нагадаємо, що при знаходженні спільного знаменника у звичайних дробів ми знаходили найменше загальне кратне знаменників, розкладаючи їх на прості множники. Аналогічно для знаходження спільного знаменника дробів алгебри може виявитися зручним розкладання знаменників на множники.

Для віднімання алгебраїчних дробів з різними знаменниками потрібно передусім привести дроби до спільного знаменника, а потім виконати операції над отриманими дробами з однаковими знаменниками.

ПРИКЛАД:

Іноді виникає потреба знайти різницю дробу і цілого виразу. Їх можна віднімати, як дроби, записавши цілий вираз у вигляді дробу із знаменником  1.

ПРИКЛАД:
Подібним способом спрощують вирази, які складаються із трьох чи більше дробів, сполучених знаками плюс чи мінус.

ПРИКЛАД:
ПРИКЛАД:

Виконайте віднімання:
РОЗВ'ЯЗАННЯ:
ПРИКЛАД:
Спростіть вираз:
РОЗВ'ЯЗАННЯ:
ПРИКЛАД:
Спростіть вираз:
РОЗВ'ЯЗАННЯ:
ПРИКЛАД:
Виконайте додавання:
РОЗВ'ЯЗАННЯ:
ПРИКЛАД:
Виконайте віднімання:
РОЗВ'ЯЗАННЯ:
ПРИКЛАД:
Виконайте віднімання:
РОЗВ'ЯЗАННЯ:
ПРИКЛАД:
Виконайте віднімання:
РОЗВ'ЯЗАННЯ:
ПРИКЛАД:

Відомо, що  a/b = 5.

Знайдіть значення виразу:
РОЗВ'ЯЗАННЯ:
ПРИКЛАД:
Виконайте додавання:
РОЗВ'ЯЗАННЯ:

2х2 + 2х = 2х(х + 1),

х2 – 1 = (х – 1)(х + 1).
Завдання до уроку 24
Інші уроки:
Автор: на

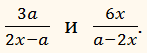
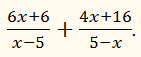
Комментариев нет:

Отправить комментарий

Подписаться на: Комментарии к сообщению (Atom)