ПРИКЛАД:
Вирішите нерівність:
РОЗВ'ЯЗАННЯ:
Знайдемо область допустимих значень вихідного нерівності
x – 5 ˃ 0, х ∈ [5; +∞).
Обидві частини вихідного нерівності невід’ємні – можна зводити в квадрат:
x – 5 < 1, x – 6 < 0,
х ∈ (–∞; 6).
Знайдемо перетин отриманого безлічі з областю допустимих значень вихідного нерівності
ВІДПОВІДЬ: [5; 6)
ПРИКЛАД:
Вирішите нерівність:
РОЗВ'ЯЗАННЯ:
Знайдемо область допустимих значень вихідного нерівності
–х ≥ 0, х ∈ (–∞;0].
Так як за визначенням квадратний корінь з будь-якого числа є величина невід’ємній і х = 0, отримаємо нерівність, еквівалентне вихідного
Отримаємо нерівність, еквівалентне вихідного
x + 1 ˃ 0.
Рішення цього нерівності
х ∈ (–1; +∞).
Знайдемо перетин отриманого безлічі з областю допустимих значень вихідній нерівності
х ∈ (–1; 0].
Враховуючи, що х = 0 не є рішенням вихідного нерівності, остаточно маємо
х ∈ (–1; 0).
ВІДПОВІДЬ: (–1; 0)
ПРИКЛАД:
Вирішите нерівність:
РОЗВ'ЯЗАННЯ:
Область допустимих значень вихідного нерівності
х ∈ [0; +∞).
Одна частина нерівності (ліва) невід’ємна, а інша (права) частина негативна.
ВІДПОВІДЬ: [0; +∞)
ПРИКЛАД:
Вирішите нерівність:
РОЗВ'ЯЗАННЯ:
Знайдемо область допустимих значень вихідного нерівності
9х – 20 ≥ 0, x ∈ [20/9; +∞).
Права частина нерівності може бути негативною, але з урахуванням області допустимих значень обидві частини нерівності невід’ємні. Отже, обидві частини нерівності звести в квадрат можна:
9х – 20 < x2,
Отримаємо
x ∈ (–∞; 4) ∪ (5; +∞).
Знайдемо перетин отриманого безлічі з областю допустимих нерівностей.
ВІДПОВІДЬ:
[20/9; 4) ∪ (5; +∞)
ПРИКЛАД:
Вирішите нерівність:
РОЗВ'ЯЗАННЯ:
Знайдемо область допустимих значень вихідний нерівності
х + 61 ≥ 0, x ∈ [–61; +∞).
Права частина нерівності
х + 5
може бути негативною. Причому область допустимих значень не виручає, як у попередньому прикладі.
1) х + 5 ≥ 0, т. е. х ∈ [–5; +∞).
В цьому випадку обидві частини нерівності невід’ємні. Отже, обидві частини нерівності можна звести в квадрат:
х + 61 < х2 + 10х + 25,
Рішення цього нерівності
х ∈ (–∞; –12) ∪ (3; + ∞).
Знайдемо перетин отриманого безлічі з безліччю
І перетин останнього безлічі з областю допустимих значень вихідного нерівності буде
х ∈ (3; +∞).
2) х + 5 < 0, тобто
х ∈ (–∞; –5).
В цьому випадку ліва частина нерівності невід’ємна, а права негативна. Така нерівність невірно, т. см. розглянутий проміжок не містить рішень вихідного нерівності.
ВІДПОВІДЬ: (3; +∞)
ПРИКЛАД:
Вирішите нерівність:
РОЗВ'ЯЗАННЯ:
Знайдемо область допустимих значень вихідного нерівності
х + 7 ≥ 0, x ∈ [–7; +∞).
Права частина нерівності може бути негативною.
1) х + 1 ≥ 0, тобто х ∈ [–1; +∞).
Зведемо обидві частини нерівності в квадрат:
х + 7 ˃ х2 + 2х + 1,
Рішення останнього нерівності
х ∈ (–3; 2).
Знайдемо перетин отриманого безлічі з безліччю
[–1; +∞)
і областю допустимих значень вихідного нерівності
це
[–1; 2).
2) х + 1 < 0, х ∈ (–∞; –1).
В цьому випадку ліва частина нерівності невід’ємна, а права негативна. Така нерівність вірно. Отже, та частина розглянутого дільниці, яка входить в область допустимих значень вихідного нерівності, є його рішенням. Знаходимо перетин розглянутого безлічі та області допустимих значень
це
[–7; –1).
Відповіддю є об'єднання відповідей, отриманих в 1) і 2) випадках:
х ∈ [–7; –1) ∪ [–1; 2), або
х ∈ [–7; 2)
ВІДПОВІДЬ: [–7; 2)
ПРИКЛАД:
Вирішите нерівність:
РОЗВ'ЯЗАННЯ:
Знайдемо область допустимих значень вихідной нерівності
х2 – х – 2 ≥ 0, (x + 1)(х – 2) ≥ 0.
Рішення цей нерівності
х ∈ (–∞; –1] ∪ [2; +∞)
Безліччю рішень вихідного нерівності є об'єднання двох безлічі: безлічі рішень суворій нерівності
і безлічі рішень рівняння
Останнє рівняння має коріння
х1 = 1, х2 = –1, х3 = 2.
Знайдемо рішення суворій нерівності
Розділимо обидві частини нерівності на позитивну величину
(значення х, звертають
в 0, не є рішеннями суворій нерівності). Отримаємо еквівалентне нерівність
х – 1 < 0.
Вирішимо його:
х < 1 або х ∈ (–∞; 1).
Отже, для остаточного результату потрібно знайти перетин безлічі (–∞; 1), коренів рівняння
з областю допустимих значень вихідного нерівності.
ВІДПОВІДЬ:
–∞ < х < –1 і х = 2.
Вирішивши
нерівність
х2
+ х – 12 ≥ 0,
знайдемо
ОДЗ початкової
нерівності, тобто множина, яка є об'єднанням проміжків
х ≥ 0 и х
< 0.
Перший випадок.
х ≥ 0, тобто х ≥
3.
х2
+ х – 12 ˃ х2,
звідки х ˃
12.
Таким чином, усі значення х з
проміжку
(12,
+∞)
х < 0,
х < 0 і х ∈
Е,
тобто
значення х з проміжку (–∞, –4], є
рішеннями початкової нерівності.
ВІДПОВІДЬ: х ≤ –4, х ˃
12
ПРИКЛАД:
Безліч Е допустимих значень (ОДЗ
нерівності) визначається
умовою
х2
– х – 2 ≥ 0,
звідки
знаходимо:
х ≤ –1, х ≥
2.
ВІДПОВІДЬ: х ≤ –1, х ≥
2
ПРИКЛАД:
ВІДПОВІДЬ: рішень
немає
ПРИКЛАД:
Ліва
частина нерівності визначена за умови
1
– х2 ≥ 0,
тобто
на множині
Е1 = [–1,
1],
а
права частина нерівності визначена за умови
3
– х2 ≥ 0,
тобто
на множині
Е2 = [–√͞͞͞͞͞3, √͞͞͞͞͞3].
Тому
ОДЗ
нерівності – перетин безлічі Е1 і Е2,
тобто множина
Е
= Е1 = [–1, 1].
4(1
– х2) < 1,
4х2 ˃ 3,
Перший спосіб.
Область
допустимих значень нерівності визначається умовою:
х2
+ 4х – 5 ≥ 0,
а
безліч Е рішень нерівності – об'єднання проміжків
(–∞, –5] і [1,
+∞).
х
∈
Е,
а
права частина міняє знак під час переходу через точку х = 5, тому слід розглянути два можливі
випадки:
х
< 5 і х
≥ 5.
1) якщо х ≥ 5, то
10
– 2х ≤ 0
2) якщо х < 5 і х ∈ Е, то обидві частини нерівностівизначені і ненегативні, тому воно рівносильне наступній нерівності
х2
+ 4х – 5 < (10 – 2х)2
а ця нерівність рівносильно наступній нерівності:
3х2 – 44х + 105
˃ 0.
Щоб вирішити цю нерівність знайдемо
корені рівняння:
3х2 – 44х + 105
= 0.
х1 = 3, х2 = 35/3.
Тому
безліч Е1
рішень нерівності
3х2 – 44х + 105
˃ 0
це
об'єднання інтервалів (–∞, 3)
і (35/3,
+∞).
Умовам х ∈
Е, х < 5 і х ∈
Е1 задовольняють
значення х з проміжків
(–∞, –5] і [1,
3).
ВІДПОВІДЬ:
х
≤ –5, 1 ≤ х < 3
Другий спосіб.
Побудуємо
графіки функцій
f(x) = g(x).
Це
рівняння – наслідок рівняння
f 2(x) = g2(x),
тобто
рівняння
х2
+ 4х – 5 = (10 – 2х)2,
яке
рівносильне рівнянню
3х2 – 44х + 105
= 0
у = 10 – 2х
перетинає графік функції y
= f(x) тільки в точці А, абсциса х0 якій – корінь рівняння
3х2 – 44х + 105
= 0,
що належить відрізку [1, 5] тобто
х0 = х1 =
3.
Відмітимо,
що корінь х2 рівняння
3х2 – 44х + 105
= 0
це
корінь рівняння
–f(x) = g(x),
тобто
абсциса точки В, в якій пряма
у
=
10
– 2х
перетинає
графік функції у = –f(x).
З
малюнка робимо висновок, що графік функції
f(x)
лежить нижче графіку функції g(x)
на проміжках:
(–∞, –5] і [1,
3).
ВІДПОВІДЬ:
Завдання до уроку 12
- Урок 1. Числові нерівності
- Урок 2. Властивості числових нерівностей
- Урок 3. Додавання і добуток числових нерівностей
- Урок 4. Числові проміжки
- Урок 5. Лінійні нерівності
- Урок 6. Системи лінійних нерівностей
- Урок 7. Нелінійні нерівності
- Урок 8. Системи нелінійних нерівностей
- Урок 9. Дробово-раціональні нерівності
- Урок 10. Рішення нерівностей за допомогою графіків
- Урок 11. Нерівність з модулем
- Урок 13. Нерівності з двома змінними
- Урок 14. Системи нерівностей з двома змінними
- Урок 15. Наближені обчислення
- Урок 16. Абсолютна і відносна погрішність



















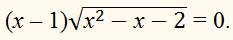
























Комментариев нет:
Отправить комментарий