ВИДЕО УРОК
Одно з проявів сили всесвітнього тяжіння – сила
тяжіння, тобто сила тяжіння тіл до Землі. Позначимо масу Землі М, її радіус R, масу цього тіла m, тоді сила, що діє на тіло поблизу поверхні Землі, згідно із законом
всесвітнього тяжіння буде рівна:
Це і є сила тяжіння. Сила тяжіння діє на тіло, тобто прикладена до самого тіла і завжди спрямована вниз, до центру Землі.
Якщо на тіло діє тільки ця сила (а усі інші урівноважені), то воно здійснює вільне падіння. Прискорення цього вільного падіння можна знайти, застосувавши другий закон Ньютона.
Звідси видно, що прискорення вільного падіннян е залежить від маси m тіла і, отже, воно однакове для усіх тел. Тепер можна написати, що сила тяжіння Сила тяжіння, що діє на тіло, дорівнює добутку маси тіла на прискорення вільного падіння.
Це і є сила тяжіння. Сила тяжіння діє на тіло, тобто прикладена до самого тіла і завжди спрямована вниз, до центру Землі.
Якщо на тіло діє тільки ця сила (а усі інші урівноважені), то воно здійснює вільне падіння. Прискорення цього вільного падіння можна знайти, застосувавши другий закон Ньютона.
Звідси видно, що прискорення вільного падіннян е залежить від маси m тіла і, отже, воно однакове для усіх тел. Тепер можна написати, що сила тяжіння Сила тяжіння, що діє на тіло, дорівнює добутку маси тіла на прискорення вільного падіння.
де F
– сила, m
– маса тіла, g – постійне число. g = 9,8 H/кг.
Іноді при розрахунках
це число можна округляти і вважати
g
= 10 H/кг.
Одиниця сили – 1
ньютон (скорочено 1
Н).
Так як сила – це
причина зміни швидкості тіла, тому за одиницю сили прийнята сила, яка за 1 сек
змінює
швидкість тіла масою 1
кг
на
1
м/сек.
Графічно силу зображують
у вигляді відрізка прямої зі стрілкою на кінці, яка вказує напрямок сили.
У деяких районах земної
кулі прискорення вільного падіння відрізняється від прийнятого. Такі відхилення
спостерігаються в тих місцях, де в надрах Землі залягають породи, щільність
яких більше або менше середньої щільності Землі. Там, де є поклади щільніших
порід, значення
більше. Це дозволяє геологам по вимірах значення
знаходити родовища
корисних копалини.
Сила тяжіння, тобто і
прискорення вільного падіння змінюються при видаленні від поверхні Землі. Якщо
тіло знаходиться на висоті h над поверхнею Землі, то вираження для
прискорення вільного падіння треба писати у виді
Так, при підйомі на
висоту 300 км прискорення вільного падіння зменшується
на 1
м/сек2. З приведеної формули видно, що при
висотах над Землею не лише в декілька десятків або сотень метрів, але навіть
багатьох кілометрів сила тяжіння може вважатися постійною, не залежною від положення
тіла. Тільки тому вільне падіння поблизу Землі і можна вважати рівноприскореним
рухом.
Рух тіла під дією сили тяжіння.
Силою тяжіння ми назвали силу всесвітнього тяжіння, з якою Земля діє на усі тіла поблизу її поверхні.
абсолютне значення якого поблизу поверхні Землі рівне 9,8 м/сек2.
ПРИКЛАД:
Спортсмен штовхає ядро, метає диск або спис, він повідомляє цим предметам саме таку початкову швидкість.
Вважатимемо, що силою опору повітря можна нехтувати. Як в цьому випадку рухається тіло ?
Показаний стробоскопічний знімок кульки, кинутої під кутом 85° до горизонту. З'єднавши послідовні положення кульки плавною лінією, отримаємо траєкторію руху кульки. Отримана траєкторія називається параболою.
Оскільки на тіло діє тільки сила тяжіння, те прискорення тіла спрямоване вертикально вниз і рівно
Проекція вектору прискорення на вісь Х дорівнює нулю, а його проекція на вісь Y негативна: g = –9,8 м/сек2. Тому через час t після початку руху тіло знаходитиметься в точці з координатами:
Прискорення сили
тяжіння залежить:
– від
маси планети;
– від
радіуса планети;
– від
висоти над поверхнею планети;
– від
географічної широти (на полюсах – 9,83 м/сек2, на екваторі – 9,79 м/сек2);
Рух тіла під дією сили тяжіння.
Силою тяжіння ми назвали силу всесвітнього тяжіння, з якою Земля діє на усі тіла поблизу її поверхні.
У відмінності від сили
пружності, яка в різних положеннях тіла різна, сила тяжіння може вважатися
постійною принаймні до висот в десятки кілометрів над Землею. Тому і
прискорення, яке сила тяжіння повідомляє тілам, теж однакове в усіх точках і
спрямоване до центру Землі.
Сила тяжіння
відрізняється від сили пружності ще і тим, що прискорення, що повідомляється
нею, не залежить від маси тіла. Тому, якщо на тіло діє тільки сила тяжіння, то,
яким би не було тіло - великим або малим, легким або важким, воно рухатиметься
з однаковим прискореннямабсолютне значення якого поблизу поверхні Землі рівне 9,8 м/сек2.
Коли початкова
швидкість тіла дорівнює нулю або спрямована паралельно силі тяжіння, тіло
здійснює вільне падіння.
Досить часто доводиться
мати справу з рухом тіл, що отримали початкову швидкість не паралельно силі
тяжіння, а спрямовану під деяким кутом до неї (чи до горизонту). Про таке тіло
говорять, що воно кинуте під кутом до горизонту.
ПРИКЛАД:
Спортсмен штовхає ядро, метає диск або спис, він повідомляє цим предметам саме таку початкову швидкість.
При
артилерійській стрільбі стволам знарядь надається деякий кут підвищення, так що
снаряд, що вилетів, теж отримує початкову швидкість, спрямовану під кутом до
горизонту.
Вважатимемо, що силою опору повітря можна нехтувати. Як в цьому випадку рухається тіло ?
Показаний стробоскопічний знімок кульки, кинутої під кутом 85° до горизонту. З'єднавши послідовні положення кульки плавною лінією, отримаємо траєкторію руху кульки. Отримана траєкторія називається параболою.
Доведемо, що тіло,
кинуте під кутом до горизонту, якщо нехтувати опором повітря, рухається по
параболі.
Вважатимемо початком
відліку (початок координат) точку, з якої було кинуто тіло, вісь Х направимо горизонтально, ост Y – вертикально
Показаний
стробоскопічний знімок кульки, кинутої під кутом 85° до горизонту. З'єднавши послідовні положення
кульки плавною лінією, отримаємо траєкторію руху кульки. Отримана траєкторія
називається параболою.
Доведемо, що тіло,
кинуте під кутом до горизонту, якщо нехтувати опором повітря, рухається по
параболі.
Вважатимемо початком
відліку (початок координат) точку, з якої було кинуто тіло, вісь Х направимо горизонтально, ост Y – вертикально
Оскільки на тіло діє тільки сила тяжіння, те прискорення тіла спрямоване вертикально вниз і рівно
Проекція вектору прискорення на вісь Х дорівнює нулю, а його проекція на вісь Y негативна: g = –9,8 м/сек2. Тому через час t після початку руху тіло знаходитиметься в точці з координатами:
x = v0x t,
де v0x і v0y
– проекції вектору початкової швидкості на осі координат
(v0x = v0 cos α и v0у = v0 sin α).
При русі тіла його координати х і у безперервно міняються з часом.
x = v0x t
і
значення часу t, що послідовно збільшуються, і вичислити координати х і у для кожного моменту часу t. По цих координатах потрібно нанести точки, які зображують послідовні положення тіла. Плавна крива, проведена через ці точки, і буде траєкторією, що цікавить нас.
Знайдемо значення ординату у тіла в цей же момент часу. Для цього підставимо у формулу знайдене значення Ми отримаємо: Підставивши в це рівняння вираження для v0x і v0y, знайдемо: Позначимо коефіцієнти при х2 і х рівність через а і b: b = tg α.
Тоді
y = ax2 + bx.
Графіком функції цього рівняння є парабола.
Тіло можна кинути і так, що його початкова швидкість буде спрямована горизонтально (α = 0). Так спрямована, наприклад, початкова швидкість тіла, що відірвалося від літака, що горизонтально летить. Легко з'ясувати по якій траєкторії стане рухатися таке тіло. Для цього звернемося до малюнка, на якому показана траєкторія руху тіла, кинутого під кутом до горизонту. У вищій точці параболи швидкість тіла якраз і спрямована горизонтально. Ми знаємо, що після цієї точки тіло рухається по правій гілці параболи. Очевидно, що і всяке тіло, кинуте з деякою початковою швидкістю спрямованою горизонтально, рухатиметься по гілці параболи. Траєкторію руху тіл, кинутих горизонтально або під кутом до горизонту, можна наочно побачити в простому досвіді.
ДОСВІД:
Бутель, наповнений водою, поміщають на деякій висоті над столом і сполучають її гумовою трубкою з наконечником, забезпеченим краном.
Струмені, що випускаються, безпосередньо показують траєкторії часток води. Вимірюючи кут, під яким випускають струмінь, можна переконатися в тому, що найбільша дальність досягається при куте 45°.
(v0x = v0 cos α и v0у = v0 sin α).
При русі тіла його координати х і у безперервно міняються з часом.
Щоб
побудувати траєкторію руху тіла, потрібно підставити в рівняння
x = v0x t
і
значення часу t, що послідовно збільшуються, і вичислити координати х і у для кожного моменту часу t. По цих координатах потрібно нанести точки, які зображують послідовні положення тіла. Плавна крива, проведена через ці точки, і буде траєкторією, що цікавить нас.
Кожному
значенню абсциси х точки траєкторії відповідає певне значення її
ординати. Тому траєкторія руху тіла є графіком залежності (графік функції) у від х, побудований в певному масштабі. Цю функцію неважко
виразити за допомогою формули.
Насправді,
ми бачили, що
x
= v0x t.
Отже, момент часу t, коли абсциса дорівнює х, визначається вираженням:Знайдемо значення ординату у тіла в цей же момент часу. Для цього підставимо у формулу знайдене значення Ми отримаємо: Підставивши в це рівняння вираження для v0x і v0y, знайдемо: Позначимо коефіцієнти при х2 і х рівність через а і b: b = tg α.
Тоді
y = ax2 + bx.
Графіком функції цього рівняння є парабола.
Тіло можна кинути і так, що його початкова швидкість буде спрямована горизонтально (α = 0). Так спрямована, наприклад, початкова швидкість тіла, що відірвалося від літака, що горизонтально летить. Легко з'ясувати по якій траєкторії стане рухатися таке тіло. Для цього звернемося до малюнка, на якому показана траєкторія руху тіла, кинутого під кутом до горизонту. У вищій точці параболи швидкість тіла якраз і спрямована горизонтально. Ми знаємо, що після цієї точки тіло рухається по правій гілці параболи. Очевидно, що і всяке тіло, кинуте з деякою початковою швидкістю спрямованою горизонтально, рухатиметься по гілці параболи. Траєкторію руху тіл, кинутих горизонтально або під кутом до горизонту, можна наочно побачити в простому досвіді.
ДОСВІД:
Бутель, наповнений водою, поміщають на деякій висоті над столом і сполучають її гумовою трубкою з наконечником, забезпеченим краном.
Струмені, що випускаються, безпосередньо показують траєкторії часток води. Вимірюючи кут, під яким випускають струмінь, можна переконатися в тому, що найбільша дальність досягається при куте 45°.
Ми розглянули декілька
прикладів руху тіл під дією сили тяжіння. З них видно, що в усіх випадках тіло
рухається з прискоренням
що повідомляється йому
силою тяжіння. Це прискорення абсолютно не залежить від того, чи рухається ще
тіло і в горизонтальному напрямі або ні. Можна навіть сказати, що в усіх цих
випадках тіло здійснює вільне падіння.
ПРИКЛАД:
Куля, випущена стрільцем з рушниці в горизонтальному напрямі, впаде на землю одночасно з кулею, випадково упущеною стрільцем у момент пострілу. Але упущена куля впаде біля ніг стрільця, а що вилетіла з рушничного ствола – в декількох сотнях метрів від нього.
На фотографії
Представлена стробоскопічна фотографія двох кульок, з яких один падає вертикально, а другому одночасно з початком падіння першого повідомлена швидкість в горизонтальному напрямі. На фотографії видно, що в один і той же момент часу (моменти спалахів світла, одночасно досягають землі).
ПРИКЛАД:
Куля, випущена стрільцем з рушниці в горизонтальному напрямі, впаде на землю одночасно з кулею, випадково упущеною стрільцем у момент пострілу. Але упущена куля впаде біля ніг стрільця, а що вилетіла з рушничного ствола – в декількох сотнях метрів від нього.
На фотографії
Представлена стробоскопічна фотографія двох кульок, з яких один падає вертикально, а другому одночасно з початком падіння першого повідомлена швидкість в горизонтальному напрямі. На фотографії видно, що в один і той же момент часу (моменти спалахів світла, одночасно досягають землі).
Розглядаючи рух тіла, кинутого
горизонтально або під кутом до горизонту, ми вважали, що воно знаходиться під
дією тільки сили тяжіння. Насправді це не так. Разом з силою тяжіння на тіло
завжди діє сила опору (тертя) з боку повітря. А вона призводить до зменшення
швидкості.
Тому дальність польоту
тіла, кинутого горизонтально або під кутом до горизонту, завжди менше, ніж це
витікає з формул. Висота підйому тіла, кинутого по вертикалі, завжди менше, ніж
вичислена по формулі.
Дія сили опору
призводить також до того, що траєкторією руху тіла, кинутого горизонтально або
під кутом до горизонту, виявляється не парабола, а складніша пряма.















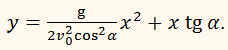









Комментариев нет:
Отправить комментарий