ВІДЕО УРОК
На підставі співвідношень між
тригонометричними функціями одного і того ж кута та визначень аркфункцій можна
отримати формули, що виражають одну аркфункцію через інші.
Нехай.
arcsin x = α
де 0
< α < π/2 и 0 < x < 1,
тоді
sin α = x.
На підставі формули
sin2 α + cos2 α
= 1
sin α = x
Порівнюючи рівності
Виразити arcsin
(–1/3) через арктангенс.
РОЗВ'ЯЗАННЯ:
arctg x = α.
де 0
< α < π/2 і x ˃ 0.
Тоді маємо:
tg α = x а ctg
α = 1/x.
Отже
α = arcctg 1/x.
Зведемо у квадрат обидві частини рівності
tg α = x,
Виразити arccos
(–2/3) через арксинус.
РОЗВ'ЯЗАННЯ:
Маємо:
arccos (–2/3) = π – arccos 2/3.
Отже,Розглянемо функцію
у = sin(arccos х).
Поклавши
arccos х
= α,
отримаємо
cos α = х.
Ми взяли перед коренем знак <<+>> тому, що
α = arccos х
задовольняє нерівностям
0 ≤ α ≤ π.
у = cos(arcsin х).
Поклавши arcsin х = α, отримаємо
sin α = х.
Тоді маємо:
Ми взяли перед коренем знак <<+>> тому, що
α = arcsin х
задовольняє нерівностям
– π/2 ≤ α
≤ π/2.
ПРИКЛАД:
Спростити
вираз:
соs (arcsin х),
де –1 ≤ х ≤ 1.
РОЗВ'ЯЗАННЯ:
Покладемо arcsin
х = у.
Тоді
sin у = х, – π/2 ≤ у ≤ π/2.
Потрібно
знайти cоs у.
Відомо
що
cоs2 у = 1 – sin2 у,
значить
cоs2 у = 1 – х2.
ПРИКЛАД:
tg[arcctg(1/9)] = 9.
ПРИКЛАД:
ctg[arctg(11/10)] = 10/11.
sin(2arccos x) =
Потрібно знайти sin
2α, але
sin 2α = 2 sin α соs α.
Обчислити:
tg
(1/2 arcсоs
(–3/5)).
РОЗВ'ЯЗАННЯ:
Покладемо
α
=
arcсоs (–3/5).
Тоді
соs
α = –3/5,
π/2 < α
< π.
Потрібно вирахувати tg
α/2.
За умовою π/2
< α
< π,
значить π/4
< α/2 < π/2,
а в інтервалі (π/4; π/2) маємо
tg
α/2 ˃ 0.
Отже tg α/2
˃ 0,
тобто
tg
(1/2 arcсоs
(–3/5))
= 2.
ПРИКЛАД:
Обчислити:
arctg(сtg
6π/5).
РОЗВ'ЯЗАННЯ:
Використовуючи рівність
сtg
6π/5 = сtg
π/5 =
tg
(π/2
– π/5) = tg 3π/10
та враховуючи, що
– π/2 < 3π/10
< π/2
arctg(сtg 6π/5)
= arctg(tg 3π/10) = 3π/10.
ПРИКЛАД:
Обчислити:
tg
(1/2
arсcos (–4/7)).
РОЗВ'ЯЗАННЯ:
Нехай
α =
arсcos (–4/7),
тоді
cos α = –4/7 , π/2 < α < π.
= sin(arcsin x) cos(arcsin y) + cos(arcsin x) sin(arcsin y) =де |х| ≤ 1 і |у| ≤ 1.
= sin(arccos x) cos(arccos y) + cos(arccos x) sin(arccos y) =де |х| ≤ 1 і |у| ≤ 1.
ПРИКЛАД:
Обчислити:
sin(arсtg
8/15
– arсcos 15/17).
РОЗВ'ЯЗАННЯ:
Нехай
α =
arсtg 8/15,
β =
arсcos 15/17.
тоді
0
< α < π/2 и tg α = 8/15,
0
< β < π/2 и cos β = 15/17.
Скористаємося
формулою
sin
(α – β) = sin α cos β – cos α sin β.
Так
як
- Урок 1. Градусний вимір кутових величин
- Урок 2. Радіанне вимірювання кутових величин
- Урок 3. Основні тригонометричні функції
- Урок 4. Натуральні тригонометричні таблиці
- Урок 5. Періодичність тригонометричних функції
- Урок 6. Область визначення і область значення тригонометричних функцій
- Урок 7. Знаки тригонометричних функцій
- Урок 8. Парність і непарність тригонометричних функцій
- Урок 9. Тригонометричні функції деяких кутів
- Урок 10. Побудова кута за даним значенням його тригонометричної функції
- Урок 11. Основні тригонометричні тотожності
- Урок 12. Вирази всіх тригонометричних функцій через одну з них
- Урок 13. Розв'язання прямокутних і рівнобедрених трикутників за допомогою тригонометричних функцій
- Урок 14. Теорема синусів
- Урок 15. Теорема косинусів
- Урок 16. Рішення косокутних трикутників
- Урок 17. Приклади рішення завдань з планіметрії із застосуванням тригонометрії
- Урок 18. Рішення практичних завдань за допомогою тригонометрії
- Урок 19. Формули зведення (1)
- Урок 20. Формули зведення (2)
- Урок 21. Формули додавання і віднімання аргументів тригонометричних функцій
- Урок 22. Формули подвійних і потрійних кутів (аргументів)
- Урок 23. Формули половинного аргументу
- Урок 24. Формули перетворень суми тригонометричних функцій в добуток
- Урок 25. Графіки функції y = sin x і y = cos x
- Урок 26. Графіки функції y = tg x і ctg x
- Урок 27. Обернені тригонометричні функції
- Урок 28. Основні тотожності зворотних тригонометричних функцій
- Урок 30. Графіки зворотних тригонометричних функцій
- Урок 31. Побудова графіків тригонометричних функцій методом геометричних перетворень












































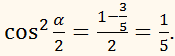













Комментариев нет:
Отправить комментарий