ВІДЕО УРОК
Перетворення
графіків функцій – це лінійні перетворення функції y = f(x) або її
аргументу х до виду
y = af(kx
+ b) + m,
а також
перетворення з використанням модуля.
Знаючи, як будувати
графіки функції y = f(x),
де
y = sin x,
y = cos x,
y = tg x,
y = ctg x,
можна побудувати графік
функції
y = af(kx + b) + m.
Перетворення графіків
тригонометричних функцій підпорядковується загальній схемі геометричних
перетворень
±k1× f(±k2× (x + a)) + b.
Паралельне перенесення
графіка вздовж осі абсцис на |b| одиниць.
y = f(x – b)
вправо, якщо b ˃ 0;
ліворуч, якщо b < 0.
y = f(x + b)
ліворуч, якщо b ˃ 0;
вправо, якщо b < 0.
ПРИКЛАД:
Побудувати
графік функції
y
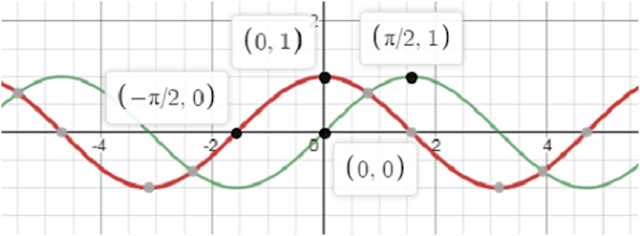
= sin (x + π/2),
користуючись
графіком
y
= sin x
РОЗВ'ЯЗАННЯ:
Зрушимо
вліво графік функції
y
= sin x
y
= sin (x + π/2)
Паралельне перенесення графіка
вздовж осі ординат на |m| одиниць.
y = f(x) + m
вгору, якщо m ˃ 0;
вниз, якщо m < 0.
Відображення графіка.
y = f(–x)
Симетричне відображення
графіка щодо осі ординат.
Стиснення та
розтягнення графіка.
Тут йдеться про
побудову графіків функцій виду:
y = m sin kx,
y = m cos kx,
y = m tg kx,
y = m ctg kx.
y = f(kx)
При k
˃ 1
– стиснення графіка до осі ординат у k разів,
при 0
<
k < 1
– розтяг графіка від осі ординат у k разів,
Взагалі кажучи,
побудова графіка функції
y = m sin kx
здійснюється у три
етапи:
1. Будують графік
функції y = sin x.
2. Будують графік
функції y = sin kx.
3.
Будують
графік функції y = m sin kx.
Аналогічно справи з
іншими тригонометричними функціями.
Насправді зазвичай при
побудові графіка функції
y = m sin kx (y
= m соs kx)
виконують розтягування
та стиск для однієї напівхвилі графіка функції
y = sin x (y
= соs x),
а потім будують весь
графік.
При побудові графіка
функції
y = m tg kx (y
= m сtg kx)
виконуються
розтягування та стиск для однієї гілки графіка функції
y = tg x (y
= сtg x),
а потім будують весь
графік.
ПРИКЛАД:
Побудувати
графік функції:
y = –3
соs 2x.
РОЗВ'ЯЗАННЯ:
Побудуємо
одну напівхвилю графіка функції
y = соs x.
Здійснивши
її стиск до осі з коефіцієнтом 2, отримаємо графік функції
y = соs 2x.
Тепер
здійснимо розтяг отриманого графіка від осі
х з
коефіцієнтом 3, а потім перетворення симетрії щодо
осі х.
В результаті ми отримаємо графік функції
y = –3
соs 2x.
Перетворення графіка із
модулем.
у = | f(x)|
При f(x) ˃ 0 – графік залишається
без змін,
при f(x) < 0 – графік симетрично
відбивається щодо осі абсцис.
Графік гармонійних
коливань у = А sin (ωx + α).
Тригонометричні функції
використовуються для опису коливальних процесів. Один з найважливіших процесів
такого роду описується формулою
у = А sin
(ωx + α).
Цю формулу називають
формулою гармонійних чи синусоїдальних коливань. Величину А називають амплітудою
коливання, вона характеризує розмах коливання. Величину ω
називають частотою коливання. Чим
більше ω, тим більше число коливань за одиницю часу (кількість коливань за
одиницю часу дорівнює ω/2π).
Нарешті α
називають
початковою фазою коливання.
Якщо, наприклад, вантаж,
що висить на пружині, вивести з положення рівноваги, він почне здійснювати
вертикальні коливання. Закон руху виражається формулою
у = А sin
(ωx + α), де
у – відхилення вантажу
від положення рівноваги,
х – час.
Той самий закон
зустрічається в теорії змінного електричного струму. При обертанні прямокутної
рамки, зробленої з провідного електричного струму матеріалу, в магнітному полі
по ній йде струм. Якщо рамка обертається рівномірно, то сила струму змінюється
за законом гармонійних коливань
у = А sin
(ωx + α).
Побудуємо графік
функції
у = А sin
(ωx + α).
Насамперед перетворимо
функцію до виду
у = А sin
(ω(x + α/ω)).
Побудова графіка цієї
функції виконаємо у кілька етапів.
1. Здійснимо паралельне
перенесення системи координат, помістивши початок нової системи х'у' у точку
О' (–α/ω; 0).
2. У системі х'у' побудуємо
графік функції
у' = sin x'
(при цьому можна
обмежитися однією напівхвильою).
3. Здійснивши стиск
побудованого графіка до осі у' з коефіцієнтом ω,
отримаємо графік
у' = sin ωx'.
4. Здійснивши розтяг
останнього графіка від осі x' з коефіцієнтом А, отримаємо необхідний графік.
ПРИКЛАД:
Побудувати
графік функції
у = 2 sin (х/3 – π/6).
РОЗВ'ЯЗАННЯ:
Маємо:
у = 2 sin (1/3
(х – π/2)).
Побудову
графіка виконаємо у кілька етапів.
1. Здійснимо паралельне перенесення системи координат, обравши початком
нової системи точку
О'
(π/2; 0).
У
системі х'у'
нам потрібно побудувати графік функції
у' = 2 sin 1/3 x'.
2. Будуємо графік функції
у' = sin x'.
3. Виконавши стиснення графіка до осі у' з коефіцієнтом
1/3 (тобто розтягнення з коефіцієнтом 3),
отримаємо графік функції
у' = sin х'/3.
4. Здійснимо розтягнення останнього графіка від осі у' з коефіцієнтом 2.
Отриманий
графік є графіком функції
ПРИКЛАД:
Побудувати
графік функції
у = 3 sin (2х + π/3).
РОЗВ'ЯЗАННЯ:
Розв'яжемо
спочатку рівняння
3 sin (2х + π/3)
= 0.
Маємо
2х + π/3 =
πk,
x
= – π/6 + πk/2,
k ∈ Z.
Дамо
параметру k два
значення: 0 та 1.
При k = 0 маємо х = – π/6.
При k = 1 маємо х = π/3.
Значить
точки
А1(–
π/6;
0) і А2(π/3; 0)
служать
кінцями однієї напівхвилі шуканої синусоїди.
Далі,
серединою відрізка [–
π/6;
π/3] є точка
π/12,
в якій функція
у
= 3 sin (2х + π/3)
приймає
максимальне значення, що дорівнює трьом. Значить
M
(π/12; 3) – точка максимуму.
Відзначаємо
на координатній площині точки
А1(–
π/6;
0),
А2(π/3; 0) і M
(π/12; 3)
- Урок 1. Градусний вимір кутових величин
- Урок 2. Радіанне вимірювання кутових величин
- Урок 3. Основні тригонометричні функції
- Урок 4. Натуральні тригонометричні таблиці
- Урок 5. Періодичність тригонометричних функції
- Урок 6. Область визначення і область значення тригонометричних функцій
- Урок 7. Знаки тригонометричних функцій
- Урок 8. Парність і непарність тригонометричних функцій
- Урок 9. Тригонометричні функції деяких кутів
- Урок 10. Побудова кута за даним значенням його тригонометричної функції
- Урок 11. Основні тригонометричні тотожності
- Урок 12. Вирази всіх тригонометричних функцій через одну з них
- Урок 13. Розв'язання прямокутних і рівнобедрених трикутників за допомогою тригонометричних функцій
- Урок 14. Теорема синусів
- Урок 15. Теорема косинусів
- Урок 16. Рішення косокутних трикутників
- Урок 17. Приклади рішення завдань з планіметрії із застосуванням тригонометрії
- Урок 18. Рішення практичних завдань за допомогою тригонометрії
- Урок 19. Формули зведення (1)
- Урок 20. Формули зведення (2)
- Урок 21. Формули додавання і віднімання аргументів тригонометричних функцій
- Урок 22. Формули подвійних і потрійних кутів (аргументів)
- Урок 23. Формули половинного аргументу
- Урок 24. Формули перетворень суми тригонометричних функцій в добуток
- Урок 25. Графіки функції y = sin x і y = cos x
- Урок 26. Графіки функції y = tg x і ctg x
- Урок 27. Обернені тригонометричні функції
- Урок 28. Основні тотожності зворотних тригонометричних функцій
- Урок 29. Вираз одній з аркфункцій через інші
- Урок 30. Графіки зворотних тригонометричних функцій






Комментариев нет:
Отправить комментарий