ВІДЕО УРОК
Графік функції аrcsin x наведено на рисунку:Графік функції Аrcsin x наведено на рисунку:
Графік функції
у
= arcsin x
симетричний щодо бісектриси І
та ІІІ
координатних кутів графіка функції:
у
= sin x, де – π/2 ≤
х ≤ π/2;
Графік функції у
= arcsin x можна отримати з графіка функції
у
= sin x, –π/2 ≤ х ≤ π/2,
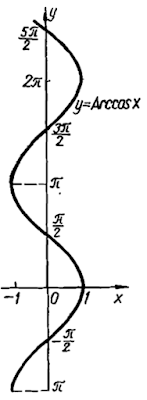
Графік функції аrcсоs x наведено на малюнку:Графік функції Аrcсоs x наведено на малюнку:Графік функції
у
= arcсоs x
симетричний щодо бісектриси І
та
ІІІ
координатних кутів графіка функції:
у
= соs x, де 0 ≤
х ≤ π;
Графік функції у
= arcсоs x може бути отриманий з графіка функції
у
= соs x, 0
≤ х ≤ π,
Графіком функції
у = arctg x служить гілка кривої х = tg у, що відповідає
проміжку зміни у від – π/2
до π/2.
у
= arctg x
симетричний щодо бісектриси І
та ІІІ
координатних кутів графіка функції
у
= tg x, де – π/2 <
х < π/2;
Графік функції у
= arctg x може бути отриманий із графіка функції
у
= tg x, –π/2 < х < π/2,
Графіком функції
у = arсctg x служить гілка кривої х = сtg у, що відповідає
проміжку зміни у від 0 до π .
у
= arсctg x.
симетричний щодо бісектриси І
та ІІІ
координатних кутів графіка функції
у
= ctg x, де 0 <
х < π
Графік функції у
= arcсtg x може бути отриманий із графіка функції
у
= сtg x, 0
< х < π,
Остання нерівність задовольняється при
х ≤ –1
і х ≥ 1
2. Область
зміни значень функції:
0 ≤ у < π/2,
у(–х) = у(х).
4. Точки перетину з осями
координат:
– з віссю Оу(х = 0) функція неспроможна мати
точок перетину, оскільки вона визначена лише за
|х| ≥ 1
5. Найменше та
найбільше значення функції в області визначення.
З
огляду на парність функції досить її досліджувати для х
≥ 1.
Якщо х
= 1,
то
у(1)
= аrcсоs 1 = 0.
тобто, найбільшого значення наша функція не має.
6. Інтервали
знакопостійності.
Оскільки функціяпарна, то досить побудувати її графік для
х
≥ 1 (1 ≤ х <
+∞),
а
потім продовжити його симетрично щодо осі Оу
для
х
≤ –1 (–∞ < х ≤
1).
[1, +∞).Продовживши його парним чином на нескінченний напівінтервал
(–∞; –1],
- Урок 1. Градусний вимір кутових величин
- Урок 2. Радіанне вимірювання кутових величин
- Урок 3. Основні тригонометричні функції
- Урок 4. Натуральні тригонометричні таблиці
- Урок 5. Періодичність тригонометричних функції
- Урок 6. Область визначення і область значення тригонометричних функцій
- Урок 7. Знаки тригонометричних функцій
- Урок 8. Парність і непарність тригонометричних функцій
- Урок 9. Тригонометричні функції деяких кутів
- Урок 10. Побудова кута за даним значенням його тригонометричної функції
- Урок 11. Основні тригонометричні тотожності
- Урок 12. Вирази всіх тригонометричних функцій через одну з них
- Урок 13. Розв'язання прямокутних і рівнобедрених трикутників за допомогою тригонометричних функцій
- Урок 14. Теорема синусів
- Урок 15. Теорема косинусів
- Урок 16. Рішення косокутних трикутників
- Урок 17. Приклади рішення завдань з планіметрії із застосуванням тригонометрії
- Урок 18. Рішення практичних завдань за допомогою тригонометрії
- Урок 19. Формули зведення (1)
- Урок 20. Формули зведення (2)
- Урок 21. Формули додавання і віднімання аргументів тригонометричних функцій
- Урок 22. Формули подвійних і потрійних кутів (аргументів)
- Урок 23. Формули половинного аргументу
- Урок 24. Формули перетворень суми тригонометричних функцій в добуток
- Урок 25. Графіки функції y = sin x і y = cos x
- Урок 26. Графіки функції y = tg x і ctg x
- Урок 27. Обернені тригонометричні функції
- Урок 28. Основні тотожності зворотних тригонометричних функцій
- Урок 29. Вираз одній з аркфункцій через інші
- Урок 31. Побудова графіків тригонометричних функцій методом геометричних перетворень





















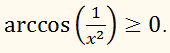







Комментариев нет:
Отправить комментарий