суббота, 12 марта 2016 г.

Урок 3. Графики

На координатной плоскости можно наглядно изобразить зависимость между разными величинами.

ПРИМЕР:

Расстояние от времени.
Температуру от времени.

Для этого на плоскости наносятся оси координат: горизонтальная – ось абсцисс и вертикальная – ось ординат. По оси абсцисс откладываются в некотором масштабе различные значения аргумента  х, или абсциссы  различных точек графика, по оси ординат – соответствующие им значения функции  у, или ординаты точек графика. Каждая пара координат, абсцисса и ордината, даёт одну точку графика. График строится по найденным характерным точкам и с учётом выявленных общих свойств зависимых величин и поведения кривых графика на различных участках. Непрерывная линия, которая соединяет эти точки, называется графиком зависимости величин. Для контроля правильности построения графика вычисляют дополнительно координаты одной или нескольких контрольных точек и наносят их на график. Контрольные точки служат также для уточнения кривых графика на отдельных участках. По графику можно находить соответствующие значения величин, анализировать.

ПРИМЕР:

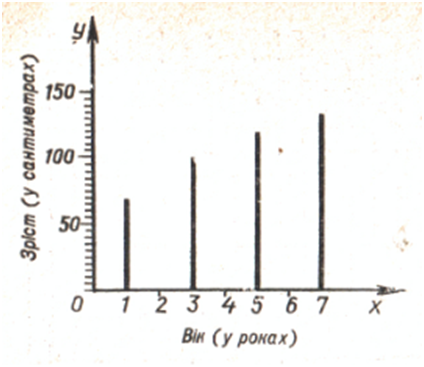
Когда Машеньки исполнился год, рост ее составлял 70 см, когда ей было 3 года – 100 см, 5 лет – 120 см и 7 лет – 135 см. По этим данным можно построить диаграмму.
На диаграмме не полностью видно, как менялся рост Машеньки: она росла все время, а на диаграмме виден ее рост только в возрасте 1, 3, 5  и  7 лет. Соединив верхние концы столбиков отрезками, достанем ломаную линию, которая лучше показывает, как менялся рост Машеньки.
Мы видим, что в  4 года ее рост примерно равнялся  110 см, а в  6,5 лет – 132 см.
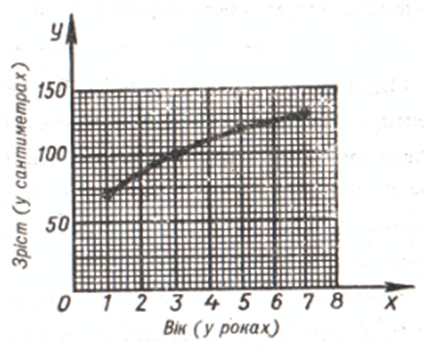
Если бы рост Машеньки измеряли все время, то образовалась бы не ломаная, а плавная линия, изображённая на рисунке.
По этой линии можно узнать о росте Машеньки в любой момент времени от  1  до  7 лет. Так, в  2 года ее рост был  90 см. Такую линию называют графиком роста Машеньки.
Чтобы точно строить графики, их чертят на миллиметровой бумаге. Например, график роста Машеньки на миллиметровой бумаге показан на рисунке.
Графики используют для изображения движения.

ПРИМЕР:

Пусть поезд, идущий со скоростью  60 км/ч, вышел в  3 часа утра из города Ромска. Тогда в  4 часа утра он будет на расстоянии 60 км от Ромска, а в  5 часов утра – на расстоянии  120 км от него и так далее. Приведенная ниже таблица показывает расстояние поезда от Ромска в разные моменты времени.
Обозначим пары чисел  (3; 0), (4; 60), (5; 120)  и т.п. точками на координатной плоскости. При этом будет удобнее выбирать разные масштабы на осях координат. Отметим на оси абсцисс единицу отрезком длиной  1 см, а на оси ординат – 60 единиц отрезком длиной  1 см. Получим точки  А, В, С, D, Е, F  и  Н.
Все эти точки лежат на одной прямой.
 Если поезд не вышел из Ромска в  3 часа утра, а прошел мимо него в это время, то таблицу можно продлить и влево:
Знак <<минус>> показывает, что поезд еще не дошел до города Ромска, а идет к нему. Точки с координатами  (0; –180), (1; –120), (2; –60)  лежат на одной прямой с ранее найденными. Эту прямую называют графиком движения поезда. По графику можно узнать, где был поезд в  5 ч 30 мин (он отошел от г. Ромска на  150 км), где он был в  1 ч 30 мин (он не дошел от г. Ромска на 90 км), когда он отошел от г. Ромска на  270 км (в 7 ч 30 мин) и т.д.

ПРИМЕР:

Вы знаете, что стоимость товару зависит от его количества: чем больше товара покупают, тем больше будет его стоимость. Если цена одного килограмма конфет стоит  35 руб., то за  2 кг необходимо заплатить 70 руб., за 3 кг – 105 руб. и т. д. Вы знаете, что такую зависимость можно наглядно отобразить на диаграмме.

Но на диаграмме тяжело определить, сколько стоит 2,5 кг конфет или другое их количество. Изобразим данные про стоимость конфет не столбиками, а вертикальными отрезками в системе координат. Так как величина  << масса конфет >>  и  << стоимость покупки >>  будут прямо пропорциональными, то верхние концы столбиков диаграммы можно соединить отрезками. Прямая показывает, как изменяется стоимость покупки в зависимости от массы конфет. Такую линию называют графиком зависимости величины  << стоимость покупки >>  от величины << масса конфет >>.
ПРИМЕР:

 Между пристанями  А  и  В, расположенными на разных берегах озера, курсирует паром. На рисунке изображён график движения парома во время движения двух первых рейсов от  А  до  В  и назад. С какой скоростью двигался паром вторым рейсом от  А  до  В ?
Из графика видно, что расстояние от пристани  А  до пристани  В  равно  8 км. Первым рейсом паром проплыл  от  пристани  А  до пристани В  за  40 мин, затем стоял у пристани  В  40 мин, после чего через  40 мин вернулся к пристани  А. Вторым рейсом паром из  А  до  В  проплыл за 
(240 – 160 = 80) мин.
Значит скорость его была:
8 км : 80 мин = 0,1 км/мин, или
0,1 км/мин × 60 мин = 6 км/час.          

 Задания к уроку 3
Другие уроки:
Автор: на

Комментариев нет:

Отправить комментарий

Подписаться на: Комментарии к сообщению (Atom)