Перш ніж приступити до рішення прикладів і завдань, обов'язково ознайомтеся з теоретичною частиною уроку
ВИРАЗИ ВСІХ ТРИГОНОМЕТРИЧНИХ ФУНКЦІЙ ЧЕРЕЗ ОДНУ З НИХ
або
ВІДЕО УРОКОМ
1. Чому дорівнює cos α, якщо sin α = 0,6 і
π/2 < α < π ?
а) 0,8;
б) sin2 α;
в) –0,8;
г) cos2 α.
а) –1;
б) 2;
в) –2;
г) 1.
3.
Визначите
тангенс гострого кута α,
якщо:
sin
α
= 0,8.
а) 4/5;
б) –4/3;
в) –4/5;
г) 4/3.
4. Знайдіть
cos α, якщо
sin α = –
4/5,
π < α < 3π/2.
а) –3/5;
б) 2/5;
в) –2/5;
г) 3/5.
5. Знайдіть
tg α, якщо
sin α = –
4/5,
π < α < 3π/2.
а) –3/4;
б) 3/4;
в) –4/3;
г) 4/3.
6. Знайдіть
ctg α, якщо
sin α = –4/5,
π
< α < 3π/2.
а) –3/4;
б) 3/4;
в) –4/3;
г) 4/3.
7. Визначите
тангенс гострого кута α,
якщо:
cos α = 0,936.
а) –44/119;
б) –44/117;
в) 44/119;
г) 44/117.
8. Визначите
тангенс гострого кута α,
якщо:
sin α = 16/65.
а) 16/63;
б) 16/65;
в) –16/63;
г) –16/65.
9. Визначите тангенс
гострого кута α,
якщо:
cos α = 65/97.
а) 72/63;
б) –72/65;
в) 72/65;
г) –72/63.
10.
Визначите
синус гострого кута α,
якщо:
tg α =
7/24.
а) –7/23;
б) 7/25;
в) –7/25;
г) 7/23.
11.
Знайдіть
значення cos α, якщо tg
α
= –3
і
а) 2 sin2 α;
б) –2;
в) 2 cos2
α;

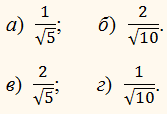

Комментариев нет:
Отправить комментарий