ВІДЕО УРОК
Основні тригонометричні
тотожності дозволяють визначити за значенням однієї з тригонометричних функцій
значення всіх інших.
ПРИКЛАД:
Відомо
що
sin
x = –3/5,
причому
π < х
< 3π/2.
Знайти
cos
x, tg x, ctg x.
РОЗВ'ЯЗАННЯ:
З
формули
sin2 α + cos2 α = 1
отримуємо
cos2 х = 1 – sin2 х.
cos2
х = 16/25
значить,
або cos х = 4/5
або cos
х = –4/5.
За умовою:
π < х
< 3π/2,
тобто аргумент х належить
третій чверті. Але в третій чверті косинус від'ємний. Значить, з двох
зазначених вище можливостей вибираємо одну:
cos
х = –4/5.
Знаючи sin x і cos х, знаходимо tg x і ctg x:
ctg x = 4/3.ВІДПОВІДЬ:
cos
х = –4/5,
tg
x = 3/4,
ПРИКЛАД:
Дано:
sin
α = 20/29.
Обчислити
значення інших тригонометричних функцій гострого кута α.
РОЗВ'ЯЗАННЯ:
З
формули:
sin2
α + соs2 α = 1
маємо:
соs2
α = 1 – sin2 α
соs
α = 21/29
tg
α = 20/29
: 21/29
= 20/21.
Звідси,
користуючись формулою
tg
α ∙
сtg α = 1,
соs
α = 21/29,
tg
α = 20/21,
сtg α = 21/20.
ПРИКЛАД:
Визначити значення тригонометричних функцій кута α, якщо
tg
α = 3/4
і 180° < α < 270°.
РОЗВ'ЯЗАННЯ:
180° < α < 270°.
Отримаємо
–sec α = 5/4
звідки
sec α = –5/4.
сos α = – 4/5.
180° < α < 270°
знаходимо
sin α = –3/5.
ВІДПОВІДЬ:
sin
α = –3/5,
соs
α = –4/5,
сtg
α = 4/3.
ПРИКЛАД:
Відомо
що
ctg
x = –5/12,
причому
π/2 <
х < π.
Знайти
sin
х,
cos x, tg x.
РОЗВ'ЯЗАННЯ:
З
формули
1 + ctg2 α = cosec2 α
sin2
х = 144/169
значить,
або sin
х = 12/13
або sin
х = –12/13.
За умовою:
π/2 <
х < π,
тобто аргумент х належить
другій чверті. Але в другій чверті синус позитивний. Значить, з двох зазначених
вище можливостей вибираємо одну:
sin
х = 12/13.
cos
x = ctg x ∙
sin х =
=
–5/12 ∙ 12/13 = –5/13.
tg
x = –12/5.
ВІДПОВІДЬ:
sin
х = 12/13,
cos
х = –5/13,
tg
x = –12/5.
ПРИКЛАД:
Дано:
сtg
α = 45/28.
Обчислити інші тригонометричні функції гострого кута α.
РОЗВ'ЯЗАННЯ:
Записуємо
значення tg α як величину, зворотну сtg
α:
tg
α = 28/45.
sin2 α + cos2 α = 1,
соs
α = сtg
α
∙ sin α.
sin
х = 28/53,
cos
х = 45/53,
tg
x = 28/45.
Співвідношення між
тригонометричними функціями одного аргументу.
У всіх формулах, в яких входять функції tg
α або sес α, виключається
значення
α
= (2k + 1) π/2,
де k
– будь-яке ціле число, так як при цих та тільки при цих значеннях α функції tg
α або sес α не визначені, тобто не існують. У всіх
формулах, в які входять функції ctg α або cosес α,
виключаються значення
α = kπ,
де k
– будь-яке ціле число, так як при цих та тільки при цих значеннях α функції ctg
α
або cosес
α не визначені (не існує).
У тих формулах, в які входять радикали, в загальному
випадку перед радикалом слід ставити подвійний знак ±.
Вибір певного знака може бути проведений, якщо дано додаткову умову.
ПРИКЛАД:
Дано:
соs
α = 2/7.
Обчислити
значення інших тригонометричних функцій гострого кута α.
РОЗВ'ЯЗАННЯ:
З
формули:
sin2
α + соs2 α = 1
Висловити
значення тригонометричних функцій гострого кута через cos
α.
РОЗВ'ЯЗАННЯ:
З
формули:
sin2
α + cos2 α = 1
ПРИКЛАД:
Висловити cos
α через всі інші тригонометричні функції кута α.
РОЗВ'ЯЗАННЯ:
З
тотожності:
sin2
α + cos2 α = 1
Далі
з рівності
sec2 α = 1 + tg2 α
Вивести
вирази тригонометричних функцій гострого кута через tg
α.
РОЗВ'ЯЗАННЯ:
sin2 α + cos2 α = 1, тозвідсиі, отже,нарешті,ПРИКЛАД:
Дано: tg
α = 7/8.
Обчислити
з точністю до 0,01 інші
тригонометричні функції кута α, якщо
π
< α < 3π/2.
РОЗВ'ЯЗАННЯ:
Маємо:
sin α ≈ –7/8 ∙ (–0,75) ≈
–0,66,
cosec α ≈ –1/0,66
≈ –1,52.
ПРИКЛАД:
Дано: ctg
α = a.
Знайти
інші тригонометричні функції кута α.
РОЗВ'ЯЗАННЯ:
Будемо
вважати, що а ≠ 0, тоді
tg α = 1/а.
Так
як
- Урок 1. Градусний вимір кутових величин
- Урок 2. Радіанне вимірювання кутових величин
- Урок 3. Основні тригонометричні функції
- Урок 4. Натуральні тригонометричні таблиці
- Урок 5. Періодичність тригонометричних функції
- Урок 6. Область визначення і область значення тригонометричних функцій
- Урок 7. Знаки тригонометричних функцій
- Урок 8. Парність і непарність тригонометричних функцій
- Урок 9. Тригонометричні функції деяких кутів
- Урок 10. Побудова кута за даним значенням його тригонометричної функції
- Урок 11. Основні тригонометричні тотожності
- Урок 13. Розв'язання прямокутних і рівнобедрених трикутників за допомогою тригонометричних функцій
- Урок 14. Теорема синусів
- Урок 15. Теорема косинусів
- Урок 16. Рішення косокутних трикутників
- Урок 17. Приклади рішення завдань з планіметрії із застосуванням тригонометрії
- Урок 18. Рішення практичних завдань за допомогою тригонометрії
- Урок 19. Формули зведення (1)
- Урок 20. Формули зведення (2)
- Урок 21. Формули додавання і віднімання аргументів тригонометричних функцій
- Урок 22. Формули подвійних і потрійних кутів (аргументів)
- Урок 23. Формули половинного аргументу
- Урок 24. Формули перетворень суми тригонометричних функцій в добуток
- Урок 25. Графіки функції y = sin x і y = cos x
- Урок 26. Графіки функції y = tg x і ctg x
- Урок 27. Обернені тригонометричні функції
- Урок 28. Основні тотожності зворотних тригонометричних функцій
- Урок 29. Вираз одній з аркфункцій через інші
- Урок 30. Графіки зворотних тригонометричних функцій
- Урок 31. Побудова графіків тригонометричних функцій методом геометричних перетворень

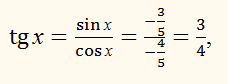









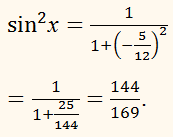




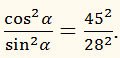







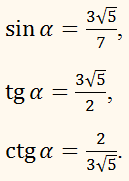




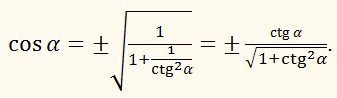
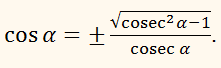

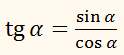
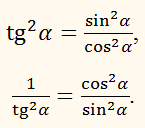


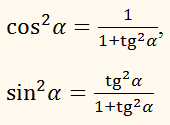





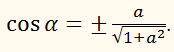

Комментариев нет:
Отправить комментарий