ВИДЕО УРОК
Для поділу дробів зберігається той же визначення, що
і для поділу цілих чисел. Розділити одне число на друге – значить знайти таке
третє число, яке при множенні на друге дає перше.
Розподіл є дією, зворотним множенню. Тобто розподіл
припускає знаходження невідомого множника, коли відомий добуток і інший множник. Цей же сенс
поділу зберігається і при розподілі звичайних дробів.
Взаємно
обернені числа.
Дві дробу, що
володіють тим властивістю, що чисельник першого є знаменником другий, а
знаменник першої є чисельником другий, називаються взаємно зворотними.
ПРИКЛАД:
Для
дробу 8/7 зворотна
дріб буде 7/8.
Число, протилежне даному числу, виходить від ділення
одиниці на дане число. Добуток взаємно зворотних чисел дорівнює одиниці.
ПРИКЛАД:
Ділення звичайного дробу на звичайний дріб.
Нехай потрібно розділити
звичайну дріб a/b на звичайну дріб c/d. Іншими словами, нам
потрібно визначити таке число, множення якого на дільник c/d дасть ділене
a/b. Це число дорівнює добутку
(d/с – число, зворотне числу c/d). Дійсно, властивості множення дозволяють нам записати такі рівності: з яких випливає, що є частка від ділення a/b на c/d.
(d/с – число, зворотне числу c/d). Дійсно, властивості множення дозволяють нам записати такі рівності: з яких випливає, що є частка від ділення a/b на c/d.
Узагальнивши всю
наведену інформацію, отримуємо правило ділення звичайних дробів:
Щоб поділити дріб на
дріб, треба чисельник першого дробу помножити на знаменник другого, а знаменник
першого помножити на чисельник другого і перший добуток записати чисельником, а
другий – знаменником.
або
Щоб розділити звичайну дріб на звичайну дріб,
потрібно ділене помножити на число, протилежне дільнику.
ПРИКЛАД: Отже, правило ділення звичайних дробів зводить розподіл до множення. Таким чином, щоб успішно виконати ділення дробів за цим правилом, треба вміти виконувати множення звичайних дробів.
Проведіть ділення дробів:
РОЗВ'ЯЗАННЯ:
ПРИКЛАД: Отже, правило ділення звичайних дробів зводить розподіл до множення. Таким чином, щоб успішно виконати ділення дробів за цим правилом, треба вміти виконувати множення звичайних дробів.
ПРИКЛАД:
Виконати
ділення дробу 9/7 на дріб 5/3.
РОЗВ'ЯЗАННЯ:
Числом, зворотним дільнику 5/3, є дріб 3/5. Тоді за правилом
ділення звичайних дробів отримуємо:
ВІДПОВІДЬ: 27/35
При необхідності треба
проводити скорочення дробу, а також виділення цілої частини з неправильного
дробу.
ПРИКЛАД:
Перейдемо від ділення дробів до множення:
Проведемо скорочення дробу: Залишилося виділити цілу частину з неправильного дробу: ВІДПОВІДЬ: 14/9
Щоб розділити звичайну дріб на ціле число,
потрібно чисельник залишити колишнім, а знаменник помножити на ціле число.
Також можна виконувати розподіл дробу на натуральне число, якщо уявити натуральне число у вигляді дробу зі знаменником 1. ПРИКЛАД:
Також можна виконувати розподіл дробу на натуральне число, якщо уявити натуральне число у вигляді дробу зі знаменником 1. ПРИКЛАД:
Розділіть
дріб 16/45 на натуральне число 12.
РОЗВ'ЯЗАННЯ:
За правилом ділення дробу на число маємо:
Виконаємо скорочення:
ВІДПОВІДЬ: 4/135
ПРИКЛАД:
Однак в даному прикладі простіше чисельник розділити на ціле число: Ділення натурального числа на звичайну дріб.
Щоб поділити ціле число на дріб, треба це ціле число помножити на знаменник даного дробу і, зробивши цей добуток чисельником, поділити його на чисельник даного дробу.
Також можна виконувати поділ натурального числа на звичайну дріб, якщо уявити натуральне число у вигляді дробу зі знаменником 1. ПРИКЛАД: ПРИКЛАД:
Виконайте
ділення натурального числа 25 на
дріб 15/28.
РОЗВ'ЯЗАННЯ:
Ділення мішаних чисел.
ПРИКЛАД:
Однак при розподілі змішаного числа на ціле іноді буває зручніше ділити окремо цілу і дробову частини змішаного числа.
Однак при розподілі змішаного числа на ціле іноді буває зручніше ділити окремо цілу і дробову частини змішаного числа.
ПРИКЛАД:
Ділення цілого числа на ціле.
Ділення цілого числа на ціле.
Щоб поділити ціле число на ціле,
треба скласти дріб, чисельник якого дорівнює діленому, а знаменник –
дільникові.
Щоб розділити суму (різницю) дробів, досить
розділити кожну з них, а потім знайти суму (різницю) отриманих часток. Щоб
розділити добуток на число, достатньо розділити тільки один з його
співмножників.
Якщо при розподілі
дробових чисел збільшити або зменшити ділене і дільник одночасно в однакове
число раз, то частка не зміниться.
Завдання до уроку 18
Інші уроки:
- Урок 1. Нумерація
- Урок 2. Додавання натуральних чисел
- Урок 3. Віднімання натуральних чисел
- Урок 4. Таблиця множення
- Урок 5. Множення натуральних чисел
- Урок 6. Ділення натуральних чисел
- Урок 7. Степінь числа
- Урок 8. Вимірювання величин
- Урок 9. Ділення с остачею
- Урок 10. Подільність натуральних чисел
- Урок 11. Найбільшій спільний дільник (НСД)
- Урок 12. Найменше спільне кратне (НСК)
- Урок 13. Звичайні дроби
- Урок 14. Перетворення дробів
- Урок 15. Додавання дробів
- Урок 16. Віднімання дробів
- Урок 17. Множення дробів
- Урок 19. Знаходження дробу від числа (задачи)
- Урок 20. Знаходження числа за відомою його частиною (задачи)
- Урок 21. Кінечни десяткові дроби
- Урок 22. Додавання десяткових дробів
- Урок 23. Віднимання десяткових дробів
- Урок 24. Множення десяткових дробів
- Урок 25. Ділення десяткових дробів
- Урок 26. Округлення чисел










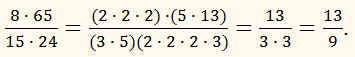















Комментариев нет:
Отправить комментарий