ВІДЕОУРОК
Паралелепіпедом називається призма, основами якої є
паралелограми.
Паралелепіпед,
бічні ребра якого перпендикулярні до площин основ, називається прямим.
– в
паралелепіпеді протилежні грані рівні і паралельні;
–
діагоналі паралелепіпеда перетинаються в одній точці і діляться в ній пополам;
– сума
квадратів всіх діагоналей паралелепіпеда дорівнює сумі квадратів усіх його
ребер;
– точка перетину
діагоналей паралелепіпеда і точка перетину діагоналей основ лежать на одній
прямій.
Поверхня прямого паралелепіпеда.
Бічною
поверхнею прямого паралелепіпеда називається сума площ всіх її бічних граней.
Повною поверхнею прямого паралелепіпеда називається сума її бічної поверхні і площ основ.
Бічна поверхня прямого паралелепіпеда дорівнює добутку периметра перпендикулярного перерізу на бічне ребро.
Бічна поверхня прямого паралелепіпеда дорівнює добутку периметра основи на висоту прямого паралелепіпеда.
ЗАДАЧА:
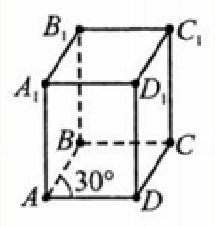
Основою
прямої призми є паралелограм зі сторонами
9 см
і 14 см
і кутом між ними 30°. Висота призми – 15
см. Обчислите площу повної поверхні призми.
Sосн
= 9 ×
14 × sin
30° =
9 × 14 × 1/2 = 63 (см2).
9 × 14 × 1/2 = 63 (см2).
Росн
= 2 ×
(AB + AD) =
= 2 × (9 + 14) = 46 (см).
= 2 × (9 + 14) = 46 (см).
Sб
= 46 ×
15 = 690 (см2).
Sп
= 2 × 63 + 690 =
= 126 + 690 = 816 (см2).
= 126 + 690 = 816 (см2).
ВІДПОВІДЬ: 816 см2.
Похилий
паралелепіпед.
Паралелепіпед, бічні ребра якого не перпендикулярні до площин
основ, називається похилим.
Властивості похилого паралелепіпеда.
– в похилом паралелепіпеді протилежні грані рівні і паралельні;
– діагоналі похилого паралелепіпеда перетинаються в одній точці
і діляться в ній пополам;
– сума квадратів всіх діагоналей похилого паралелепіпеда
дорівнює сумі квадратів усіх його ребер;
Поверхня похилого
паралелепіпеда.
Бічною
поверхнею похилого паралелепіпеда називається сума площ всіх її бічних граней.
Повною поверхнею похилого паралелепіпеда називається сума її бічної поверхні і площ основ.
Бічна поверхня похилого паралелепіпеда дорівнює добутку периметра перпендикулярного перерізу на бічне ребро.
ЗАДАЧА:
Основа
похилого паралелепіпеда – квадрат зі стороною
а. Одна з вершин другої основи
проектується в центр цього квадрата. Висота паралелепіпеда дорівнює Н. Знайти бічну поверхню
паралелепіпеда.
Нехай
основою похилого паралелепіпеда
ABCDA1B1C1D1
є квадрат ABCD зі стороною АВ = а, О – центр цього квадрата, А1О = Н – висота паралелепіпеда.
Проведемо ОК
⊥
АD,
ОМ ⊥
АВ. Тоді за теоремою про
три перпендикуляри ABCDA1B1C1D1
є квадрат ABCD зі стороною АВ = а, О – центр цього квадрата, А1О = Н – висота паралелепіпеда.
А1К ⊥ АВ, А1M ⊥ АВ,
тобто А1К і А1M – висоти бічних граней
ADD1A1 та ABB1A1
відповідно. Прямокутні трикутники A1OK та A1OM рівні (A1O – спільний катет і ОК = ОМ = a/2), звідки A1K = A1M . Оскільки, крім того, AD = AB, то
З ∆ A1OM (∠ O = 90°).
Отже,
ВІДПОВІДЬ:
ЗАДАЧА:
В
основі похилого паралелепіпеда лежить прямокутник. Бічне ребро утворює із
суміжними сторонами основи кути, кожний з яких дорівнює по 60°. Знайти кут, який утворює це бічне
ребро з площиною основи паралелепіпеда.
Нехай ABCDA1B1C1D1
– заданий похилий паралелепіпед. ABCD
– прямокутник,
∠ A1AD = ∠ A1AB = 60°,
A1K – висота паралелепіпеда.
∠ A1AD = ∠ A1AB = 60°,
A1K – висота паралелепіпеда.
∠ AA1N = 90° – 60° = 30°.
Отже, AN = 1/2 AA1. Аналогічно у
∆ A1MA ∠ AA1M = 30°,
тому AM = 1/2 AA1. Оскільки
AN = AM = 1/2 AA1, то
AMNK – квадрат і прямокутний трикутник ANK – рівнобедрений.
Отже, ∠ A1АM = 45°.
ВІДПОВІДЬ: 45°.
Завдання до уроку 5
Інші уроки:
- Урок 1. Прямі і площині у просторі
- Урок 2. Пряма призма
- Урок 3. Похила призма
- Урок 4. Правильна призма
- Урок 6. Прямокутний паралелепіпед
- Урок 7. Куб
- Урок 8. Піраміда
- Урок 9. Правильна піраміда
- Урок 10. Зрізана піраміда
- Урок 11. Циліндр
- Урок 12. Вписана і описана призма
- Урок 13. Конус
- Урок 14. Зрізаний конус
- Урок 15. Вписана і описана піраміда
- Урок 16. Сфера і куля
- Урок 17. Комбінації тіл











Комментариев нет:
Отправить комментарий