ВИДЕО УРОК
Додавання дробів з однаковими знаменниками.
Спочатку розберемо складання дробів з однаковими знаменниками. Отримати правило складання дробів нам допоможе наступний приклад.
ПРИКЛАД:
Нехай на тарілку поклали три восьмих частки яблука і після цього ще дві восьмих частки такого ж яблука.
В результаті на тарілці виявилося
3 + 2 = 5 восьмих часток яблука,
тобто, тобто 5/8. Таким чином, додавання звичайних
дробів 3/8 і 2/8 дає звичайну дріб 5/8.
З розглянутого прикладу можна зробити висновок, що додавання дробів з однаковими знаменниками дає дріб, чисельник якого дорівнює сумі числівників складаються дробів, а знаменник дорівнює знаменників вихідних дробів.
Сумою дробів з одним і
тим же знаменником називають дріб, що має той же знаменник, а чисельник
дорівнює сумі числівників даних дробів.
Запишемо це правило складання дробів за
допомогою букв. Нехай нам потрібно виконати додавання звичайного дробу a/b і звичайного дробу c/b. Тоді згідно з правилом
складання дробів з однаковими знаменниками справедливо рівність:Це визначення можна сформулювати також у вигляді наступного правила.
Щоб скласти дробу з однаковими знаменниками, треба скласти їх чисельники і залишити той же знаменник.
Всі закони і властивості складання натуральних чисел справедливі і для дробових чисел. Їх застосування в багатьох випадках значно спрощує процес обчислення.
Сума дрібних чисел підпорядковується переставному закону. Сума дрібних чисел підпорядковується сполучному закону. Якщо який-небудь доданок збільшимо або зменшимо на яке-небудь число, то
і сума збільшиться чи зменшиться на те ж саме число.
ПРИКЛАД:
Складіть звичайні дроби:
5/23 + 7/23.
РОЗВ'ЯЗАННЯ:
Знаменники складаються дробів рівні, тому в результаті складання буде дріб з таким же знаменником 23, а її чисельник дорівнюватиме сумі чисельників складаються дробів, тобто,
5 + 7 = 12.
Отже, складання дробів 5/23 і 7/23 призводить нас до дробу 12/23. Коротко рішення записується так
ВІДПОВІДЬ: 12/23
Якщо складання дробів дає скороченість дроби, то потрібно провести скорочення дробу. Якщо при цьому отримана дріб неправильна, то потрібно виділити з неї цілу частину.
ПРИКЛАД:
Обчисліть суму звичайних дробів:
5/28 + 3/28.
РОЗВ'ЯЗАННЯ:
Застосувавши правило складання дробів з однаковими знаменниками, отримаємо:
Очевидно, отриману дріб можливо скоротити, так як чисельник і знаменник діляться на 2. Виконаємо скорочення дробу:
Таким чином, складання дробів 5/28 і 3/28 дає 2/7.
ВІДПОВІДЬ: 2/7
ПРИКЛАД:
Виконайте додавання звичайних дробів:
15/62 + 140/62.
РОЗВ'ЯЗАННЯ:
Проведемо рішення дробів з однаковими знаменниками:
Перевіримо, чи можна скоротити отриману дріб. Для цього обчислимо найбільший спільний дільник її чисельника і знаменника. Найзручніше скористатися алгоритмом Евкліда:
155 = 62 ∙ 2 + 31,
62 = 31 ∙ 2.
Отже
НСД (155, 62) = 31.
Таким чином, дріб 155/62 можна скоротити на 31.
Очевидно, дріб 5/2 неправильна. Виконавши виділення цілої частини з неправильного дробу 5/2, отримуємо 2 1/2.
Отже, весь процес складання дробів з однаковими знаменниками 15/62 і 140/62 можна записати так:
ВІДПОВІДЬ: 2 1/2
ПРИКЛАД:
1/9 + 2/9 + 4/9 + 5/9 = 12/9 = 4/3 = 11/3.
Додавання дробів з різними знаменниками.
Додавання дробів з різними знаменниками можна звести до додавання дробів з однаковими знаменниками. Для цього достатньо складаються дробу привести до спільного знаменника.
Виходячи з цих міркувань, отримуємо наступний
порядок складання дробів з різними знаменниками, яке містить наступні кроки:
– складаються дробу приводяться до спільного
знаменника (зазвичай до найменшого спільного знаменника);
– виконується складання отриманих дробів з
однаковими знаменниками.
Іди іншими словами:
Щоб скласти дробу з різними знаменниками, потрібно попередньо привести їх до найменшого спільного знаменника, скласти їх чисельники і підписати спільний знаменник.
ПРИКЛАД:
Складіть звичайні дроби:
РОЗВ'ЯЗАННЯ:
Знаменники складаються дробів різні, тому спочатку потрібно виконати приведення дробів до найменшого спільного знаменника. Для цього знаходимо
НСК (8; 12) = 34.
Потім знаходимо відповідні додаткові множники:
24 : 8 = 3,
34 : 12 = 2
дробів
5/8 і 1/12.
В результаті отримаємо:
Тепер складаємо дроби
15/24 і 2/24.
Отримаємо:
Таким чином, складання дробів з різними знаменниками 5/8 і 1/12 дає дріб 17/24. Запишемо всі рішення коротко:
ВІДПОВІДЬ: 17/24
Якщо при додаванні дробів виходить скоротна дріб і (або) неправильна дріб, то потрібно провести скорочення дробу і при можливості виділити цілу частину.
ПРИКЛАД:
Виконайте додавання дробів з різними знаменниками:
РОЗВ'ЯЗАННЯ:
Для складання дробів з різними знаменниками, спочатку наведемо їх до найменшого спільного знаменника:
Тепер складемо дроби
36/15 і 10/15,
отримаємо:
Перевіримо, чи можливо отриману дріб скоротить. Для цього обчислимо найбільший спільний дільник чисельника і знаменника, скориставшись способом Евкліда:
46 = 15 ∙ 3 + 1,
15 = 1 ∙ 15,
отже
НСД (46; 15) = 1.
Але дріб 46/15 неправильна, тому з неї потрібно виділити цілу частину. Так як:
46 : 15 = 3
(залишок 1), то
Запишемо всі рішення коротко:
ВІДПОВІДЬ: 31/15
ПРИКЛАД:
Додати дроби:
РОЗВ'ЯЗАННЯ:
Знаходимо НОК (15,18)
НСК (15,18) = 3 ∙ 2 ∙ 3 ∙ 5 = 90.
Знаходимо додаткові множники для кожного дробу. Для цього найменший спільний дільник ділимо по черзі на знаменник кожного дробу.
90 : 15 = 6 – додатковий множник для дробу 3/15.
90 : 18 = 5 –
додатковий множник для дробу 4/18.
Отримані числа і будуть додатковими множниками для кожної з дробів. Множники записуємо над чисельником дробу праворуч зверху:
Чисельник і знаменник кожного дробу множимо на свій додатковий множник, користуючись основною властивістю дробу. Утворені дроби з однаковими знаменником, складаємо.
Перевіряємо отриману дріб.
Якщо
в результаті вийшла неправильна дріб, то результат записуємо у вигляді
змішаного числа.
38 < 90, дріб правильна.
Якщо в результаті вийшла скоротна дріб, необхідно виконати скорочення.
Запишемо всі рішення коротко:
ВІДПОВІДЬ: 19/45
ПРИКЛАД:
Коротше записують так:
ПРИКЛАД: Додавання звичайного дробу і натурального числа.
Додавання натурального числа з правильною звичайної дробом не представляє інтересу, так як така сума за визначенням є змішане число.
ПРИКЛАД:
Додавання натурального числа з неправильною звичайної дробом можна проводити через додавання двох дробів, якщо натуральне число замінити дробом.
Коротше записують так:
ПРИКЛАД: Додавання звичайного дробу і натурального числа.
Додавання натурального числа з правильною звичайної дробом не представляє інтересу, так як така сума за визначенням є змішане число.
ПРИКЛАД:
Додавання натурального числа з неправильною звичайної дробом можна проводити через додавання двох дробів, якщо натуральне число замінити дробом.
ПРИКЛАД:
Додавання натурального числа і неправильного дробу доцільніше проводити, виділивши з дробу цілу частину. В результаті додавання натурального числа і дроби зводиться до складання натурального числа і змішаного числа.
Додавання натурального числа і неправильного дробу доцільніше проводити, виділивши з дробу цілу частину. В результаті додавання натурального числа і дроби зводиться до складання натурального числа і змішаного числа.
ПРИКЛАД:
Додавання мішаних чисел.
При складання мішаних чисел виконуються переставний і сполучний закони додавання. Їх застосування у багатьох випадках значно спрощує процес обчислення. Властивості складання дозволяють привести складання змішаних чисел до складання їх цілих частин і до складання їх дрібних частин.
Щоб скласти змішані числа, треба спочатку скласти між собою цілі числа, а потім дробові.
ПРИКЛАД:
Скласти дроби:
РОЗВ'ЯЗАННЯ:
Щоб скласти змішані числа потрібно:
3 + 4 = 7,
– окремо скласти дробові частини (якщо у дрібних частин знаменники різні, то спочатку наводимо їх до спільного знаменника, а потім складаємо);
– скласти отримані результати (якщо при додаванні дрібних частин вийшла неправильна дріб, то потрібно виділити цілу частину з цього дробу і додати до отриманої цілої частини);
ПРИКЛАД:
ПРИКЛАД: Додавання трьох і більшої кількості звичайних дробів.
Складіть чотири звичайні
дроби:
РОЗВ'ЯЗАННЯ:
Додавання мішаних чисел.
При складання мішаних чисел виконуються переставний і сполучний закони додавання. Їх застосування у багатьох випадках значно спрощує процес обчислення. Властивості складання дозволяють привести складання змішаних чисел до складання їх цілих частин і до складання їх дрібних частин.
Щоб скласти змішані числа, треба спочатку скласти між собою цілі числа, а потім дробові.
ПРИКЛАД:
Скласти дроби:
РОЗВ'ЯЗАННЯ:
Щоб скласти змішані числа потрібно:
– окремо скласти їх цілі частини;
3 + 4 = 7,
– окремо скласти дробові частини (якщо у дрібних частин знаменники різні, то спочатку наводимо їх до спільного знаменника, а потім складаємо);
– скласти отримані результати (якщо при додаванні дрібних частин вийшла неправильна дріб, то потрібно виділити цілу частину з цього дробу і додати до отриманої цілої частини);
ПРИКЛАД:
ПРИКЛАД: Додавання трьох і більшої кількості звичайних дробів.
Додавання трьох,
чотирьох і так далі дробів можна проводити аналогічно додаванню трьох і більше
натуральних чисел.
ПРИКЛАД:
Нам потрібно обчислити суму:
Послідовно замінюючи дві сусідні дробу їх сумою, отримаємо:
Залишилося лише скоротити отриману дріб, після чого виділити цілу частину: ВІДПОВІДЬ: 12/3
Обчисліть суму:
РОЗВ'ЯЗАННЯ:
Послідовно замінюючи дві сусідні дробу їх сумою, отримаємо:
Залишилося лише скоротити отриману дріб, після чого виділити цілу частину: ВІДПОВІДЬ: 12/3
Аналогічно проводиться
складання кількох натуральних чисел і декількох звичайних дробів.
ПРИКЛАД:
Властивості додавання
дозволяють провести таку угруповання доданків:
Сума трьох натуральних чисел в дужках дорівнює 14, а сума дробів:
Таким чином: ВІДПОВІДЬ: 1411/12
Складіть три дроби з
різними знаменниками:
РОЗВ'ЯЗАННЯ:
Сума трьох натуральних чисел в дужках дорівнює 14, а сума дробів:
Таким чином: ВІДПОВІДЬ: 1411/12
Правило складання
дробів з однаковими знаменниками, і правило складання дробів з різними
знаменниками залишаються справедливими для трьох і більшої кількості
складаються дробів.
ПРИКЛАД:
Спочатку виконаємо
приведення трьох дробів до найменшого спільного знаменника:
Тепер складемо ці числа:
ВІДПОВІДЬ: 111/24
Тепер складемо ці числа:
ВІДПОВІДЬ: 111/24
Завдання до уроку 15
Інші уроки:
- Урок 1. Нумерація
- Урок 2. Додавання натуральних чисел
- Урок 3. Віднімання натуральних чисел
- Урок 4. Таблиця множення
- Урок 5. Множення натуральних чисел
- Урок 6. Ділення натуральних чисел
- Урок 7. Степінь числа
- Урок 8. Вимірювання величин
- Урок 9. Ділення с остачею
- Урок 10. Подільність натуральних чисел
- Урок 11. Найбільшій спільний дільник (НСД)
- Урок 12. Найменше спільне кратне (НСК)
- Урок 13. Звичайні дроби
- Урок 14. Перетворення дробів
- Урок 16. Віднімання дробів
- Урок 17. Множення дробів
- Урок 18. Ділення дробів
- Урок 19. Знаходження дробу від числа (задачи)
- Урок 20. Знаходження числа за відомою його частиною (задачи)
- Урок 21. Кінечни десяткові дроби
- Урок 22. Додавання десяткових дробів
- Урок 23. Віднимання десяткових дробів
- Урок 24. Множення десяткових дробів
- Урок 25. Ділення десяткових дробів
- Урок 26. Округлення чисел














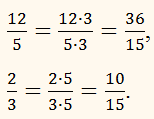
































Комментариев нет:
Отправить комментарий