Урок 18. Параллелограмм

ВИДЕОУРОК

Параллелограмм – четырёхугольник, у которого противоположные стороны параллельны (т. е. лежат на параллельных прямых).

Например,  АВСD – параллелограмм, так как 

АВ ॥ СD, BC ॥ AD.

Основные свойства параллелограмма.

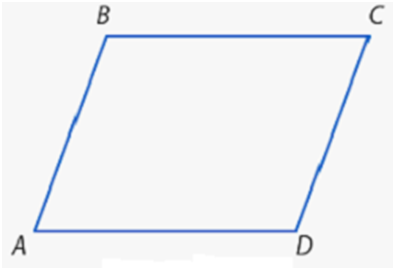
– противоположные стороны равны;

– противоположные стороны параллельны;

– диагонали делятся в точке пересечения пополам;

– противоположные углы равны.

Наличие у четырёхугольника одного из этих свойств или равенства или параллельности одной пары противоположных сторон вызывает, как следствие, все остальные свойства.

 Признаки параллелограмма.

– если две стороны четырёхугольника равны и параллельны, то этот четырёхугольник – параллелограмм;

– если противоположные стороны четырёхугольника попарно равны, то этот четырёхугольник – параллелограмм;

– если в четырёхугольнике диагонали пересекаются и в точке пересечения делятся пополам, то этот четырёхугольник – параллелограмм, а точка пересечения диагоналей является его центром симметрии;

– сумма углов, прилегающих к одной стороне равна  180°;

– диагональ делит параллелограмм на два равных треугольника;

– сумма квадратов диагоналей параллелограмма равна сумме квадратов ого сторон.

Высотою параллелограмма называют перпендикуляр, опущенный из любой точки одной стороны на противоположную сторону или её продолжение.    

– в параллелограмме угол между высотами равен его острому углу;

– биссектрисы углов, прилежащих к одной стороне параллелограмма, взаимно перпендикулярны;

– биссектрисы двух противоположных углов параллелограмма параллельны.

ЗАДАЧА:

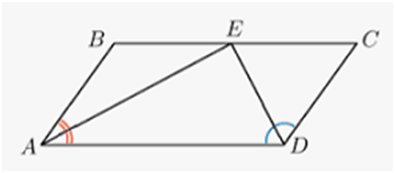
Один из углов параллелограмма равен  45°. Его высота, опущенная из вершины тупого угла, равна  3 см  и  делит сторону параллелограмма пополам. Найдите эту сторону параллелограмма.

РЕШЕНИЕ:

∠ 1 = 90° – 45° = 45°,

АЕ = ВЕ = 3 (см).

АD = 2 ∙ АЕ = 2 ∙ 3 = 6 (см).

ЗАДАЧА:

Разность двух углов параллелограмма равна  20°. Найдите меньший угол параллелограмма.

РЕШЕНИЕ:

Обозначим меньший угол – х, тогда больший будет  х + 20°.

Составим уравнение:

х + х + 20° = 180°.

Решим его:

2х = 160°, х = 80°.

ЗАДАЧА:

Сумма двух углов параллелограмма равна  168°. Найти его углы.

РЕШЕНИЕ:

Два заданных угла могут быть только противоположные углы параллелограмма, так как сумма углов, которые прилегают до одной стороны равна  180°. Поэтому, эти углы по

168° : 2 = 84°

(противоположные углы параллелограмма равны).

Тогда каждый из остальных углов по

180° – 84° = 96°.

ОТВЕТ:  84°, 96°.

ЗАДАЧА:

Стороны треугольника равны  8 см, 9 см  и  13 см. Найдите медиану треугольника, проведённую до наибольшей стороны.

РЕШЕНИЕ:

Пусть  АВС – заданный треугольник,

в котором 

ВС = 8 см,

АВ = 9 см,

АС = 13 см,

ВМ – медиана, поэтому 

МС = ¹/₂ АС.

Отложим на продолжении медианы  ВМ 

МD = ВМ.

Получим параллелограмм  АВСD  (диагонали четырёхугольника точкою пересечения делятся  пополам).

На основании формулы

запишем:

ВD² + АС² = 2(АВ² + ВС²),

Найдём  ВD:

ВD² + 13² = 2(9² + 8²),

ВD² = 121, ВD = 11.

Теперь найдём медиану  ВМ:

ВМ = 0,5 ∙ ВD = 5,5 см.

ЗАДАЧА:

Стороны треугольника равны  6 см  и  8 см. Медиана треугольника, проведённая до третьей стороны, равна  √͞͞͞͞͞46 см. Найдите неизвестную сторону треугольника.

РЕШЕНИЕ:

Пусть  АВС – заданный треугольник,

ВО – медиана,

ВС = 6 см,

АВ = 8 см,

ВО = √͞͞͞͞͞46 см.

На луче  ВО  построим отрезок  ОD  так, что  ОВ = ОD. В четырёхугольнику  АВСD  диагонали точкою пересечения делятся пополам, поэтому этот четырёхугольник будет параллелограммом. По свойству диагоналей параллелограмма получим:

АС² + ВD² = 2АВ² + 2ВС²,

Найдём  АС:

АС² + (2√͞͞͞͞͞46)² = 2(8² + 6²),

АС² = 200 – 184 = 16,

АС = 4 (см).

Задания к уроку 18

• Задание 1
• Задание 2
• Задание 3

Другие уроки:

• Урок 1. Точка и прямая
• Урок 2. Угол
• Урок 3. Параллельные и перпендикулярные прямые
• Урок 4. Окружность
• Урок 5. Угол и окружность
• Урок 6. Треугольник (1)
• Урок 7. Треугольник (2)
• Урок 8. Прямоугольный треугольник (1)
• Урок 9. Прямоугольный треугольник (2)
• Урок 10. Равнобедренный треугольник (1)
• Урок 11. Равнобедренный треугольник (2)
• Урок 12. Периметр треугольника
• Урок 13. Периметр равнобедренного (равностороннего) треугольника
• Урок 14. Треугольник и окружность
• Урок 15. Прямоугольный треугольник и окружность
• Урок 16. Равнобедренный треугольник и окружность
• Урок 17. Четырёхугольники
• Урок 19. Периметр параллелограмма
• Урок 20. Прямоугольник
• Урок 21. Периметр прямоугольника
• Урок 22. Квадрат
• Урок 23. Ромб
• Урок 24. Периметр ромба
• Урок 25. Трапеция
• Урок 26. Равнобедренная трапеция
• Урок 27. Периметр трапеции
• Урок 28. Четырёхугольник и окружность (1)
• Урок 29. Четырёхугольник и окружность (2)
• Урок 30. Многоугольник
• Урок 31. Правильный многоугольник
• Урок 32. Осевая и центральная симметрии

Завдання 3. Площа трапеції

Перш ніж приступити до рішення прикладів і завдань, обов'язково ознайомтеся з теоретичною частиною уроку

ПЛОЩА ТРАПЕЦІЇ

або

ВІДЕОУРОКОМ

 1. Точка перетину бісектрис тупих кутів при меншій основі трапеції належить більшій основі. Знайдіть площу трапеції, якщо її бічні сторони дорівнюють  25 см  і  30 см, а висота – 24 см.

 а)  988 см²;        
 б)  1086 см²;     

 в)  1048 см²;      
 г)  1020 см².

 2. Основи трапеції дорівнюють  2 см  і  7 см, а її діагоналі – 10 см  і  17 см. Знайдіть площу трапеції.

 а)  36 см²;      
 б)  32 см²;     

 в)  46 см²;      
 г)  38 см².

 3. Знайти площу трапеції, у якої паралельні сторони  60 см  і  20 см, а непаралельні – 13 см  і  37 см.

 а)  516 см²;      
 б)  520 см²;     

 в)  426 см²;      
 г)  480 см².

 4. Основи трапеції дорівнюють  11 см  і  4 см, а діагоналі – 9 см  і  12 см. Знайдіть площу трапеції.

 а)  56 см²;      
 б)  54 см²;     

 в)  52 см²;      
 г)  48 см².

 5. Точка перетину бісектрис гострих кутів при більшій основі трапеції належить її меншій основі. Знайдіть площу трапеції, якщо її бічні сторони дорівнюють  15 см  і  41 см, а висота – 9 см.

 а)  716 см²;      
 б)  778 см²;     

 в)  738 см²;      
 г)  692 см².

 6. Знайдіть площу трапеції, основи якої дорівнюють  21 см  і  30 см, бічні сторони – 12 см  і  15 см.

 а)  316 см²;      
 б)  302 см²;     

 в)  292 см²;      
 г)  306 см².

 7. Точка перетину бісектрис тупих кутів при меншій основі трапеції належить більшій основі. Знайдіть площу трапеції, якщо її бічні сторони дорівнюють  10 см  і  17 см, а висота – 8 см.

 а)  130 см²;      
 б)  132 см²;     

 в)  152 см²;      
 г)  133 см².

 8. Основи трапеції дорівнюють  2 см  і  6 см, а бічні сторони – 13 см  і  15 см. Знайдіть площу трапеції.

 а)  48 см²;      
 б)  38 см²;     

 в)  46 см²;      
 г)  50 см².

 9. Точка перетину бісектрис тупих кутів при меншій основі трапеції належить її більшій основі. Знайдіть площу трапеції, якщо її бічні сторони дорівнюють  13 см  і  15 см, а висота – 12 см.

 а)  262 см²;      
 б)  240 см²;      

 в)  216 см²;      
 г)  252 см².

10. Основи трапеції дорівнюють  6  і  16 см. Одна з бічних сторін дорівнює  10 см  і утворює з більшою основою кут  60°. Знайдіть площу трапеції.

 а)  55√͞͞͞͞͞3 см²;      
 б)  64 см²;     

 в)  72√͞͞͞͞͞3 см²;      
 г)  40 см².

11. Основи трапеції дорівнюють  3  і  8 см. Одна з бічних сторін дорівнює  5 см  і утворює з меншою основою кут  120°. Знайдіть площу трапеції.

 а)  15,75√͞͞͞͞͞3 см²;     

 б)  16,4 см²;     

 в)  12,5 см²;     

 г)  13,75√͞͞͞͞͞3 см².

12. Точка перетину бісектрис гострих кутів при більшій основі трапеції належить меншій основі. Знайдіть площу трапеції, якщо її бічні сторони дорівнюють  17 см  і  25 см, а висота – 15 см.

 а)  860 см²;      
 б)  850 см²;     

 в)  840 см²;      
 г)  835 см².

Завдання до уроку 9

• Завдання 1
• Завдання 2