ВІДЕО УРОК
Умовимося, як це прийнято, позначати елементи прямолінійного трикутника з вершинами А, В, С такими буквами А, В, С – внутрішні кути трикутника;
a, b, c
– відповідні сторони, протилежні до кутів трикутника;
ha, hb, hc
– висоти трикутника відносно сторін a, b і с;
ba, bb, bc
– бісектриси внутрішніх кутів;
S
– площа трикутника;
R
– радіус описаного кола;
r
– радіус вписаного кола;
ra, rb, rc
– радіуси зовні вписаних кіл.
Основні теореми та
формули при співвідношення між елементами трикутника.
Основними випадками
розв’язання трикутників називаються задачі на обчислення елементів трикутника
за трьома його даними незалежними основними елементами.
До основних елементів
відносять сторони і внутрішні кути трикутника, причому кути зв’язані між собою
співвідношенням
А + В + С = π,
тому тільки два з них
можуть бути незалежними.
Розв'язання
косокутного трикутника по стороні і двох кутів.
В трикутнику АВС дано: сторона
а і кути
В і С.
Знайти кут А і сторони
b і с.
Якщо дано два кути
трикутника, то третій визначаємо як
А =180° – (В + С).
sin А = sin [180° – (В + С)] =
sin (В + С),
Дано:
а
= 400,
А
= 36°40',
В
=
79°50'.
Знайти b,
с,
С.
РОЗВ'ЯЗАННЯ:
1) С = 180° – (А + В),
ПЕРЕВІРКА:
Розв'язання
косокутного трикутника з обох сторін і кута, що проти лежить одній з них.
ПРИКЛАД:
Нехай
у трикутнику АВС дано: сторони а, b і кут А. Потрібно знайти сторону с
і кути
В
і С.
РОЗВ'ЯЗАННЯ:
С
=
180° – (А + В).
На кресленнірозглянуто випадок, коли кут А – гострий. На наступному кресленнірозглянуто випадок, коли цей кут тупий. У цьому випадку завдання або не має рішення (І) або має лише одне рішення (ІІ).
Нехай кут А – гострий. Тоді як випливає з кресленняв разі
а
< b sin А
завдання
не має рішення (I), у
разі
а
= b sin А
завдання
має одне рішення (II),
якщо
b
˃
а ˃ b sin А,
Завдання
має два рішення (III), нарешті, якщо а ≥ b, Завдання має одне рішення (IV).
Дано:
а = 242,
b = 767,
В = 36°53'.
Знайти с, А, С.
РОЗВ'ЯЗАННЯ:
2) С = 180° – (А + В),
ПРИКЛАД:
Дано:
а = 400,
b = 500,
А = 40°.
Знайти с, В, С.
РОЗВ'ЯЗАННЯ:
180° – 53°28' = 126°32'.
Кут
С
буде інший, а у зв'язку із цим зміниться
і сторона с. Позначимо ці нові значення
відповідно через
В', С', с'.
Маємо:
1) В' = 126°32'.
2) С' =
180° – (А + В'),
а = 400,
b = 500,
А = 40°,
один
з них – гострокутний, інший – тупокутний. Побудова трикутника при цих даних
підтверджує отримані дві відповіді.
ПРИКЛАД:
Дано:
а = 165,
b = 268,
А = 53°08'.
Знайти с, В, С.
РОЗВ'ЯЗАННЯ:
Маємо
b sin
А ≈ 268 ∙ 0,8000 ˃ а = 165,
Отже,
завдання немає рішень.
Формули
для визначення кута трикутника з двох його сторін та кута між ними.
З прямокутного
трикутника АВD
отримуємо співвідношення
З трикутника ВСD знаходимо:
h
= a sin C
і далі:
AD = AC – DC,
DC = a cos C.
Рівність
AD = AC – DC
тепер представиться в
такому вигляді:
AD = b – a
cos C.
Вираз для h з рівності
h
= a sin C
і AD з рівності
AD = b – a
cos C
h
= a sin (180° – C) = a sin C,
а
СD
= a соs (180° – C) = –a соs C.
На підставі
h
= a sin C
і
СD
= –a соs C
ПРИКЛАД:
У
трикутнику АВС дано: сторони а і b та кут С.
Знайти сторону с і кути А
і В.
РОЗВ'ЯЗАННЯ:
1-й спосіб. За
теоремою косинусів маємо:
c2 = a2
+ b2 – 2ab cos C.
Звідки
отримаємо с.
цей
гострий кут В, знаходимо кут А:
А = 180° – (В + С).
B = 180° – (A + С).
Кожен із цих способів може бути використаний для
перевірки рішення іншим способом.
ПРИКЛАД:
Дано: а
= 320, b = 400, С = 110°21'.
Знайти с, А і В.
РОЗВ'ЯЗАННЯ:
Перший
метод.
1)
По теоремі косинусів маємо:
c2 = a2
+ b2 – 2ab cos C.
Звідки
отримаємо с:
c2 = 3202 + 4002 – 2 ∙ 320 ∙
400 cos 110°21'
=
3202 + 4002
– 2 ∙ 320 ∙
400 cos 69°39' ≈
102 400
+ 256 000 ∙ 0,3478 ≈ 351 437.
ПЕРЕВІРКА:
110°21'
+ 30°24' + 39°15'
= 180°.
2) А = 180° – (В
+ С),
Візьмемо трикутник АВС. Впишемо в нього коло
радіусу r. Центр О це кола знаходиться на перетині бісектрис
внутрішніх кутів трикутника.
AD = AF = k,
BD = BE = m,
CE = CF = n.
Якщо проведемо радіуси
OD, OE, OF
в точки дотику, то
утворюються шість прямокутних трикутників.
a + b + c = 2k + 2m + 2n.
Якщо периметр
трикутника позначимо через 2p,
то отримаємо
2p = 2k
+ 2m + 2n,
звідки
p = k + m + n.
Так як m + n = a, то з рівності
p = k + m + n
отримаємо, що
k = p – a.
Так як A, B, C
–
кути трикутника, половини їх A/2, B/2,
C/2 – завжди кути гострі. Тому
tg
A/2, tg
B/2, tg
C/2
позитивні.
Формули
визначення кутів трикутника з трьох його сторонам з допомогою теореми косинусів.
Теорема косинусів дає таку залежність між трьома
сторонами трикутника та кутом:
a2 = b2
+ с2 – 2bс cos А.
У трикутнику АВС дано сторони а, b,
с. Потрібно знайти кути А,
В і С трикутника. Кути А, В і С трикутника можна
визначити за формулами, що виражають
cos А, cos В, cos C
tg А/2, tg В/2, tg С/2.
Дано: а = 13, b = 18, с
= 15.
Знайти А, В і С.
РОЗВ'ЯЗАННЯ:
ПЕРЕВІРКА:
А
+ В + С =
45°16' + 79°40' + 55°4'
= 180°.
Другий
спосіб.
Маємо:
2р = 13 + 18 + 15 = 4,
р
= 23,
р
– а =10,
р
– b = 5,
р
– с = 8.
ПЕРЕВІРКА:
(р – а) + (р – b)
+ (р – с) =
розкриємо
дужки
р
– а + р – b + р – с
=
згрупуємо
та наведемо подібні члени
3р – (а + b + с)
=
Так
як (а + b
+ с)
це периметр Р
= 2р, то
одержуємо:
3р – 2р = р.
- Урок 1. Градусний вимір кутових величин
- Урок 2. Радіанне вимірювання кутових величин
- Урок 3. Основні тригонометричні функції
- Урок 4. Натуральні тригонометричні таблиці
- Урок 5. Періодичність тригонометричних функції
- Урок 6. Область визначення і область значення тригонометричних функцій
- Урок 7. Знаки тригонометричних функцій
- Урок 8. Парність і непарність тригонометричних функцій
- Урок 9. Тригонометричні функції деяких кутів
- Урок 10. Побудова кута за даним значенням його тригонометричної функції
- Урок 11. Основні тригонометричні тотожності
- Урок 12. Вирази всіх тригонометричних функцій через одну з них
- Урок 13. Розв'язання прямокутних і рівнобедрених трикутників за допомогою тригонометричних функцій
- Урок 14. Теорема синусів
- Урок 15. Теорема косинусів
- Урок 17. Приклади рішення завдань з планіметрії із застосуванням тригонометрії
- Урок 18. Рішення практичних завдань за допомогою тригонометрії
- Урок 19. Формули зведення (1)
- Урок 20. Формули зведення (2)
- Урок 21. Формули додавання і віднімання аргументів тригонометричних функцій
- Урок 22. Формули подвійних і потрійних кутів (аргументів)
- Урок 23. Формули половинного аргументу
- Урок 24. Формули перетворень суми тригонометричних функцій в добуток
- Урок 25. Графіки функції y = sin x і y = cos x
- Урок 26. Графіки функції y = tg x і ctg x
- Урок 27. Обернені тригонометричні функції
- Урок 28. Основні тотожності зворотних тригонометричних функцій
- Урок 29. Вираз одній з аркфункцій через інші
- Урок 30. Графіки зворотних тригонометричних функцій
- Урок 31. Побудова графіків тригонометричних функцій методом геометричних перетворень















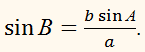















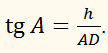



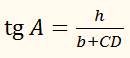






















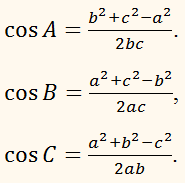





Комментариев нет:
Отправить комментарий