ВИДЕО УРОК
Умножение обыкновенной дроби на обыкновенную дробь.
ПРИМЕР:
Найти значение выражения:Получили ответ.
Сокращаем данную дробь. Дробь можно сократить на 2. Тогда окончательное
решение примет следующий вид:Это действие можно
понимать, как взятие пиццы от половины пиццы. Допустим, у нас есть а пиццы:Как взять от этой половины две третьих ?
Сначала нужно поделить эту половину на три
равные части:И взять от этих трёх
кусочков два:У нас получится одна
треть всей пиццы. Вспомните как выглядит пицца, разделённая на три части:Один кусок от этой пиццы
и взятые нами два кусочка будут иметь одинаковые размеры:Другими словами, речь
идёт об одном и том же размере пиццы. Поэтому значение выражения равно:Произведением дробей называют такую дробь, числитель которой равен произведению числителей данных дробей, а знаменатель – произведению их знаменателей.Чтобы умножить дробь на дробь, нужно умножить числитель на числитель, а знаменатель на знаменатель и первое произведение сделать числителем, а второе – знаменателем произведения.
При умножении следует делать (если возможно) сокращение.
ПРИМЕР:
Приведём пример, иллюстрирующий правило умножения обыкновенных дробей.
ПРИМЕР:
Рассмотрим квадрат со стороной 1 ед., при этом его площадь равна 1 ед2.
Разделим этот квадрат на равные прямоугольники со сторонами 1/4 ед. и 1/8 ед., при этом исходный квадрат будет состоять из
4 ∙ 8 = 32
прямоугольников. Следовательно, площадь каждого прямоугольника составляет 1/32 долю площади исходного квадрата, то есть она равна 1/32 ед2. Теперь закрасим часть исходного квадрата.
Стороны закрашенного прямоугольника равны 5/8 ед. и 3/4 ед., значит, его площадь равна произведению дробей 5/8 и 3/4, то есть,
Но закрашенный прямоугольник состоит из 15 маленьких прямоугольников, значит его площадь равна 15/32 ед2. Следовательно,
Так как
5 ∙ 3 = 15
8 ∙ 4 = 32,
то последнее равенство можно переписать как
что подтверждает формулу умножения обыкновенных дробей.
С помощь этого правила умножения можно умножать и правильные и неправильные дроби, и дроби с одинаковыми знаменателями, и дроби с разными знаменателями.
ПРИМЕР:
Выполните умножение обыкновенной дроби 7/11 на обыкновенную дробь 9/8.
РЕШЕНИЕ:
Произведение числителей умножаемых дробей 7 и 9 равно 63, а произведение знаменателей 11 и 8 равно 88. Таким образом, умножение обыкновенных дробей 7/11 и 9/8 даёт дробь 63/88.
ОТВЕТ: 63/88
Помните про сокращение полученной дроби, если в результате умножения получается сократимая дробь, и при выделении целой части из неправильной дроби.
ПРИМЕР:
Выполните умножение обыкновенной дроби 4/15 на обыкновенную дробь 55/6.
РЕШЕНИЕ:
Применим правило умножения обыкновенных дробей:
Очевидно, что полученная дробь сократима. Выполним сокращение дроби.
НОД (220; 90) = 10.
Осталось выделить целую часть из полученной неправильной дроби:
Краткая запись решения:
ОТВЕТ: 24/9
Осталось выделить целую часть из полученной неправильной дроби:
Краткая запись решения:
ОТВЕТ: 24/9
Сокращение дроби можно проводить до вычисления произведений числителей и произведений знаменателей умножаемых дробей, то есть когда дробь имеет вид
Для этого числа
a, b, c, d
заменяют их разложениями на простые множители, после чего сокращаются одинаковые множители числителя и знаменателя.
Решим предыдущий пример другим способом.
ПРИМЕР:
Выполните умножение обыкновенной дроби 4/15 на обыкновенную дробь 55/6.
РЕШЕНИЕ:
Применим правило умножения обыкновенных дробей:
Так как
4 = 2 ∙ 2,
55 = 11 ∙ 5,
15 = 5 ∙ 3,
6 = 2 ∙ 3, тоТеперь сокращаем общие простые множители:
Вычислим произведения в числителе и знаменателе дроби, после чего выделим целую часть из неправильной дроби.
Краткая запись решения:
ОТВЕТ: 24/9
Для умножения дробей характерно переместительное свойство, то есть умножаемые дроби можно менять местами:
Умножение обыкновенной дроби на натуральное число.
Смысл умножения обыкновенной дроби на натуральное число выясняется из следующего определения: умножить обыкновенную дробь (множимое) на натуральное число (множитель) – значит найти эту дробь множимого.
Чтобы умножить натуральное число на дробь, надо умножить натуральное число на числитель дроби и это произведение сделать числителем, а знаменателем подписать знаменатель данной дроби.
С помощью букв правило умножение дроби a/b на натуральное число n имеет вид:
Эта формула следует из формулы умножения двух обыкновенных дробей:Представив натуральное число как дробь со знаменателем 1, получим:
Если учесть, что целое число представляет собой дробь со знаменателем 1, то умножение дроби на целое число и целого числа на дробь можно выполнить по этому же правилу.
ПРИМЕР:
ПРИМЕР:
ПРИМЕР:
Умножение числителя 2 на число 5 даёт 10, поэтому в силу правила умножения дроби на натуральное число, произведение 2/27 на 5 равно дроби 10/27.
ОТВЕТ: 10/27
ПРИМЕР:
ПРИМЕР:
Выполните умножение дроби 2/27 на 5.
РЕШЕНИЕ:
ОТВЕТ: 10/27
При умножении дроби на натуральное число полученную дробь часто приходится сокращать, а если она ещё и неправильная, то представить её в виде смешанной дроби.
ПРИМЕР:
Выполните умножение дроби 5/12 на 8.
РЕШЕНИЕ:
По формуле умножения дроби на натуральное число имеем:
Полученная дробь сократима. Выполним сокращение дроби. Так как НОК (40; 12) = 4, то
Осталось выделить целую часть:
Краткое решение примера:
Сокращение можно было провести, заменив числа в числителе и знаменателе их разложением на простые множители. В этом случае решение выглядело бы так:
ОТВЕТ: 31/3
Умножение дроби на натуральное число обладает переместительным свойством, то есть произведение дроби на натуральное число, равно произведению этого натурального числа на дробь.
Умножение смешанных чисел.
Чтобы перемножить смешанные числа, нужно предварительно обратить их в неправильные дроби и потом перемножить по правилу умножения дроби на дробь.
Если же перемножают смешанное число на целое, то проще множить отдельно целую и дробную части.
ПРИМЕР:
Законы и правила умножения натуральных чисел справедливы и для дробей. Их использование упрощает устные и письменные вычисления.
Прежде чем вычислить произведения в числителе и знаменателе, целесообразно заменить все множители их разложениями на простые множители и провести сокращение:
ОТВЕТ: 9/280
Законы и правила умножения натуральных чисел справедливы и для дробей. Их использование упрощает устные и письменные вычисления.
Произведение дробных чисел подчиняется переместительному, сочетательному и распределительному закону.
Если один из сомножителей – целое число, то умножение может быть выполнено на основании распределительного закона.
ПРИМЕР:
42/5 ∙ 3 = (4 + 2/5) ∙ 3
= 4 ∙ 3 + 2/5 ∙ 3
= 12 + 6/5 = 131/5.
ПРИМЕР:
97/8 ∙ 8 = 9 ∙ 8 + 7/8 ∙ 8
= 72 + 7 = 79.
Если один из двух сомножителей увеличим в несколько раз, а другой оставим без изменения, то произведение увеличится во столько же раз.
Если один из сомножителей уменьшим в несколько раз, а другой оставим без изменения, то произведение уменьшится во столько же раз.
Умножение трёх и большего количества дробей.
Свойства умножения натуральных чисел распространяются и на умножение дробей.
Переместительное и сочетательное свойства умножения позволяют однозначно определить умножение трёх и большего количества дробей. При этом всё происходит по аналогии с умножением трёх и большего количества натуральных чисел. В частности, дроби и натуральные числа в произведении можно для удобства вычисления переставлять местами, а при отсутствии скобок, указывающих порядок выполнения действий, можно самим расставить скобки любым из доступных способов.
ПРИМЕР:
3/4 ∙ (79/31 ∙ 11/3) =
(3/4 ∙ 4/3) ∙ 79/31 =
1 ∙ 79/31 = 79/31.
ПРИМЕР:
(122/5 ∙ 435/17) ∙ 5/31 =
(122/5 ∙ 5/31) ∙ 435/17
= 2 ∙ 435/17 = 8610/17.
ПРИМЕР:
Выполните умножение четырёх обыкновенных дробей:
1/20, 12/5, 3/7, 5/8.
РЕШЕНИЕ:
Запишем произведение, которое нам нужно вычислить:
В силу правила умножения дробей записанное произведение равно дроби, числитель которой равен произведению числителей всех дробей, а знаменатель – произведению знаменателей.Прежде чем вычислить произведения в числителе и знаменателе, целесообразно заменить все множители их разложениями на простые множители и провести сокращение:
ОТВЕТ: 9/280
ПРИМЕР:
Выполните умножение пяти чисел:
РЕШЕНИЕ:
Задания к уроку 17
Другие уроки:
- Урок 1. Нумерация
- Урок 2. Сложение натуральных чисел
- Урок 3. Вычитание натуральных чисел
- Урок 4. Таблица умножения
- Урок 5. Умножение натуральных чисел
- Урок 6. Деление натуральных чисел
- Урок 7. Степень числа
- Урок 8. Измерение величины
- Урок 9. Деление с остатком
- Урок 10. Делимость натуральных чисел
- Урок 11. Наибольший общий делитель (НОД)
- Урок 12. Наименьшее общее кратное (НОК)
- Урок 13. Обыкновенные дроби
- Урок 14. Преобразование дробей
- Урок 15. Сложение дробей
- Урок 16. Вычитание дробей
- Урок 18. Деление дробей
- Урок 19. Нахождение дроби от числа (задачи)
- Урок 20. Нахождение числа по известной его части (задачи)
- Урок 21. Конечные десятичные дроби
- Урок 22. Сложение десятичных дробей
- Урок 23. Вычитание десятичных дробей
- Урок 24. Умножение десятичных дробей
- Урок 25. Деление десятичных дробей
- Урок 26. Округление чисел
































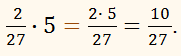













Комментариев нет:
Отправить комментарий