вторник, 4 июля 2017 г.

Урок 21. Взаимное расположение графиков линейных функций

Графики двух линейных функций представляют собой прямые, которые либо пересекаются, либо параллельны.

Графики двух линейных функций, заданных формулами вида

y = kx + b, 

пересекаются, если коэффициенты при  х  различны, и параллельны, если коэффициенты при  х  одинаковы.

Докажем это.

Пусть  y = k1x + b1  и  y = k2x + b2 – две различные линейные функции. Чтобы выяснить, каково взаимное расположение их графиков, рассмотрим уравнение

k1x + b1 = k2x + b2

Имеем

k1x – k2x = b2 – b1,

(k1 – k2) x = b2 – b1.

Если  k1 ≠ k2, то это уравнение имеет единственный корень. В этом случае графики функций пересекаются.
Если  k1 = k2  и  b1 ≠ b2, то уравнение не имеет корней. В этом случае графики функций параллельны.
ПРИМЕР:

Даны графики функций, заданных формулами:

у = 0,9х – 1,
у = 0,8х + 1

с различными коэффициентами при  х.
Выясним, пересекаются ли эти графики. Пересечение графиков означает, что они имеют общую точку. В этом случае найдётся такое значение х, которому соответствует одно и то же значение  у  для обеих функций. Чтобы найти это значение  х, надо решить уравнение

0,9х – 1 = 0,8х + 1.

Имеем:

0,9х – 0,8х = 1 + 1,
0,1х = 2,
х = 20.

При  х = 20  обе функции

у = 0,9х – 1,
у = 0,8х + 1

принимают одно и то же значение, равное  17. Точка  (20; 17)  принадлежит как одному, так и другому графику. Такая точка только одна. Значит, прямые, являющиеся графиками функций

у = 0,9х – 1,
у = 0,8х + 1

пересекаются.

ПРИМЕР:

Даны графики функций, заданных формулами:

у = 0,5х + 1,
у = 0,5х – 2

с одинаковыми коэффициентами при  х.
Чтобы выяснить, пересекаются ли графики этих функций, надо решить уравнение

0,5х + 4 = 0,5х – 2.

Так как это уравнение не имеет корней, то прямые, которые являются графиками функций

у = 0,5х + 1,
у = 0,5х – 2

Не имеют общих точек, т. е. они параллельны.

На рисунке изображены прямые, которые являются графиками линейных функций, заданных формулами вида

y = аx + b, 

с одинаковыми коэффициентами при  х  и различными значениями  b.
Все эти прямые параллельны и наклонены к оси  х  под одним и тем же углом. Этот угол зависит от коэффициента  а. Число  а  называют угловым коэффициентом прямой – графика функции

y = аx + b, 

используя термин угловой  коэффициент прямой, доказанное выше свойство можно сформулировать так:

– если угловые коэффициенты прямых, являющихся графиками двух линейных функций, различны, то эти прямые пересекаются, а если угловые коэффициенты одинаковы, то прямые параллельны.

Из формулы

y = аx + b, 

Следует, что при  х = 0  значение  у  равно  b. Значит, график функции  y = аx + b  пересекает ось  у  в точке с координатами  (0; b). На рисунке изображены прямые, которые являются графиками функций, заданных формулами вида  y = аx + b  с различными  а  и одним и тем же значением  b. Все эти прямые пересекаются в одной точке, лежащей на оси  у.

ПРИМЕР:

При каких значениях  k  и  b  график линейной функции  y = kx + b  пересекается с графиком функции

у = 12х + 18 ?

k =12, b = 20,

k =12, b = 18,

k =14, b = 18,

k =18, b = 12.

РЕШЕНИЕ:

Если угловые коэффициенты прямых, являющихся графиками двух линейных функций, различны, то эти прямые пересекаются. Значит при  k =14, b = 18  и  k =18, b = 12  прямые пересекаются.

ПРИМЕР:

Выберите функции, графики которых параллельны графику функции:

у = 0,7х + 0,3.

у = 1,7х + 0,3,

у = 0,7х,

у = 0,3х + 0,7,

у = 0,7х + 2,3.

РЕШЕНИЕ:

Если угловые коэффициенты одинаковы, то прямые параллельны, значит, параллельны графику функции  у = 0,7х + 0,3  будут следующие функции  у = 0,7х, у = 0,7х + 2,3.

ПРИМЕР:

График некоторой линейной функции вида  y = kx + 1  параллелен графику функции  y = –0,4x. Найдите значение коэффициента  k  и выясните, принадлежит ли этому графику точка  М(50; – 19).

РЕШЕНИЕ:

Так как прямые параллельны, значит, угловые коэффициенты у них равны, k = –0,4. Тогда функция  y = kx + 1  будет выглядеть следующим образом:

y = –0,4x + 1.

Подставим координаты точки  М  в это уравнение:

–19 = –0,4 ∙ 50 + 1,  –19 = –19.

ОТВЕТ:  точка  М  принадлежит этому графику

ПРИМЕР:

Задайте формулой линейную функцию, графиком которой служит прямая, проходящая через точку  А(2; 3)  и параллельная графику функции  y = 1,5x – 3.

РЕШЕНИЕ:

Так как прямые параллельны, значит, угловые коэффициенты у них равны, k = 1,5. Тогда функция  y = kx + b  будет выглядеть следующим образом:

y = 1,5x + b.

Найдём  b:

b = 1,5x – у.

Подставим в это уравнение координаты точки  А:

b = 1,5 ∙ 2 – 3 = 0.

Значит формула будет выглядеть следующим образом:

у = 1,5х.

ПРИМЕР:

Найдите точку пересечения прямых:

у = 2х – 3  и  у = 2 – 1/2 х.

РЕШЕНИЕ:

Для линейной функции  у = 2х – 3  имеем:
Прямая  l1, служащая графиком линейной функции  у = 2х – 3  показана на рисунке через точки  (0; –3)  и  (2; 1).
Для линейной функции  у = 2 – 1/2 х  имеем:
Прямая  l2, служащая графиком линейной функции  у = 2 – 1/2 х  показана на рисунке через точки  (0; 2)  и  (2; 1).
ОТВЕТ:  точкой пересечения прямых будет точка с координатами  (2; 1).

ПРИМЕР:

Найдите точку пересечения прямых:

у = 2х – 3  и  у = 2 – 3 х.

РЕШЕНИЕ:

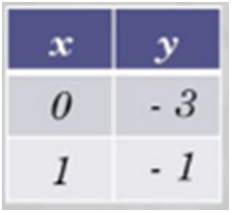
Первый способ: графический.

Построим графики функций в одной системе координат.

Для функции  у = 2х – 3  имеем:
Для функции  у = 2 – 3 х  имеем:
Из графика видно, что точка пересечения имеет координаты

А(1; –1).

Второй способ: аналитический.

Угловые коэффициенты прямых различны, значит прямые пересекаются в одной точке. Эта общая точка имеет координату  (х0; у0). Приравняв правые части и решив уравнение, мы найдём абсциссу точки пересечения.

2х0 – 3 = 2 – 3х0,

2х0 + 3х0 = 2 + 3,

5х0 = 5,  х0 = 1.

Чтобы найти ординату, подставим полученное значение аргумента  х0  в одну из функций:

у0 = 2х0 – 3 = 2 ∙ 1 – 3 = – 1.

ОТВЕТ:  А(1; –1)

Задания к уроку 21
Другие уроки:
Автор: на

Комментариев нет:

Отправить комментарий

Подписаться на: Комментарии к сообщению (Atom)