Прежде чем приступить к решению примеров и задач, обязательно ознакомьтесь с теоретической частью урока
ПРЯМОУГОЛЬНЫЙ ТРЕУГОЛЬНИК (1)
или посмотрите
ВИДЕОУРОК
1. Из точки к прямой проведена наклонная прямая, длина которой равна 12 см. Найдите проекцию наклонной на прямую, если наклонная образует с прямой угол 30°.
а) √͞͞͞͞͞2 см;
б) 12√͞͞͞͞͞3 см;
в) 6√͞͞͞͞͞2 см;
б) 12√͞͞͞͞͞3 см;
в) 6√͞͞͞͞͞2 см;
г) 6√͞͞͞͞͞3 см.
2. Из точки М до прямой а проведён перпендикуляр МN и наклонная МК. Найдите длину проекции наклонной, если
2. Из точки М до прямой а проведён перпендикуляр МN и наклонная МК. Найдите длину проекции наклонной, если
МN = 12 см, МК = 13 см.
а) 6 см;
б) 1 см;
в) 5 см;
г) 25 см.
б) 1 см;
в) 5 см;
г) 25 см.
3. Верхнюю точку электрической опоры из
точки, которая находится на расстоянии 12 м от её основания,
видно под углом 45°. Какая высота опоры ?
а) 6 м;
б) 12 м;
а) 6 м;
б) 12 м;
в) 18 м;
г) 24 м.
г) 24 м.
4. Из точки до прямой проведено две наклонных
прямые длиной 10
см и 18
см, а сумма их проекций на прямой
равна 16
см. Найти расстояние от данной
точки до прямой.
а) 3√͞͞͞͞͞11 см;
б) √͞͞͞͞͞34 см;
в) 2√͞͞͞͞͞11 см;
г) 7 см.
5. В треугольнике АВС,
∟С = 90°,
ВС = 5 см,
АС = 3 см.
Найдите АВ.
∟С = 90°,
ВС = 5 см,
АС = 3 см.
Найдите АВ.
а) 2√͞͞͞͞͞34 см;
б) √͞͞͞͞͞34 см;
в) √͞͞͞͞͞43 см;
г) 4 см.
6. В
треугольнике АВС,
∟С = 90°,
ВС = 5 см,
АВ = 10 см.
Найдите АС.
∟С = 90°,
ВС = 5 см,
АВ = 10 см.
Найдите АС.
а) 5√͞͞͞͞͞3 см;
б) 5 см;
в) 5√͞͞͞͞͞5 см;
б) 5 см;
в) 5√͞͞͞͞͞5 см;
г) 3√͞͞͞͞͞3 см.
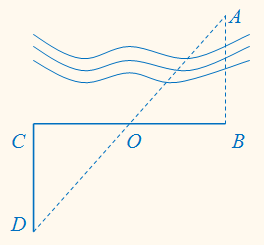
7. Чтобы измерить расстояние от пункта В до недоступного пункта А, с помощью прибора построили прямой угол АВС и на его стороне отметили точки О и С так, что ВО = ОС. Затем построили прямой угол ВСD и на его стороне нашли такую точку D, которая лежит и на прямой АО. Измерив СD, утверждали, что СD = АВ. Верно ли такое измерение ?
7. Чтобы измерить расстояние от пункта В до недоступного пункта А, с помощью прибора построили прямой угол АВС и на его стороне отметили точки О и С так, что ВО = ОС. Затем построили прямой угол ВСD и на его стороне нашли такую точку D, которая лежит и на прямой АО. Измерив СD, утверждали, что СD = АВ. Верно ли такое измерение ?
8. Разность двух острых углов
прямоугольного треугольника равна одному из них. Найдите эти острые углы.
а) 35°, 70°;
б) 20°, 40°;
б) 20°, 40°;
в) 40°, 50°;
г) 30°, 60°.
г) 30°, 60°.
9. Средняя линия треугольника АВС образует с
АВ углы, которые вдвое больше углов при этой
стороне. Найдите углы треугольника.
а)
40°, 50°;
б) 45°, 45°;
в) 30°, 60°;
г) 35°, 55°.
10. Две средние линии треугольника равны между собой и взаимно перпендикулярны. Определите градусную меру углов треугольника.
а) 40°, 50°;
б) 45°, 45°;
в) 30°, 60°;
г) 35°, 55°.
10. Две средние линии треугольника равны между собой и взаимно перпендикулярны. Определите градусную меру углов треугольника.
а) 40°, 50°;
б) 45°,
45°;
в) 30°, 60°;
г) 35°, 55°.
в) 30°, 60°;
г) 35°, 55°.
11. В прямоугольном треугольнике гипотенуза равна 9 см,
а один из катетов – 6 см,
Найдите проекцию данного катета на гипотенузу.
а) 6 см;
б) 1,5 см;
в) 3 см;
г) 4 см.
б) 1,5 см;
в) 3 см;
г) 4 см.
12. Катет
равен 28 см, разность
двух других сторон 8 см. Определите
гипотенузу.
а) 53 см;
б) 61 см;
в) 51 см;
г) 45 см.
б) 61 см;
в) 51 см;
г) 45 см.
Комментариев нет:
Отправить комментарий