ВИДЕОУРОК
3 × 4 = 12 (см2).
ЗАДАЧА:
Длина прямоугольника
0,7 дм,
а ширина 0,3
дм. Найдите площадь прямоугольника.
РЕШЕНИЕ:
Чтобы найти площадь прямоугольника, необходимо его длину умножить
на ширину:
0,7 ∙ 0,3 = 0,21 (дм2).
ЗАДАЧА:
Стороны прямоугольника
3,2 см и 4,8 см. Найдите его площадь.
РЕШЕНИЕ:
Решим эту задачу сначала, пользуясь правилом умножения
натуральных чисел. Для этого выразим данные в миллиметрах:
3,2 см = 32 мм,
4,8 см = 48 мм.
Длины сторон прямоугольника выражаются теперь натуральными
числами, поэтому его площадь найдём, перемножив эти числа:
32 ∙ 48 = 1536 (мм2).
Выразим найденную площадь в квадратных сантиметрах. Так
как
1 см2 = 100 мм2, то
1 мм2 = 1/100 см2,
поэтому
1536 мм2 = 1536/100 см2
=
= 1536/100 см2
= 15,36
см2.
ОТВЕТ;
Длина прямоугольника
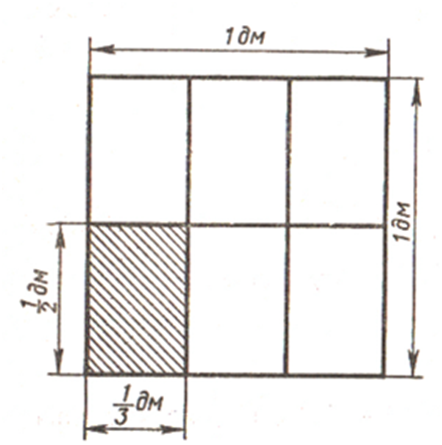
1/2 дм, а ширина 1/3 дм. Найдите площадь прямоугольника.
РЕШЕНИЕ:
1/2 ∙ 1/3 = 1/6 (дм2).
ЗАДАЧА:
Длина прямоугольника
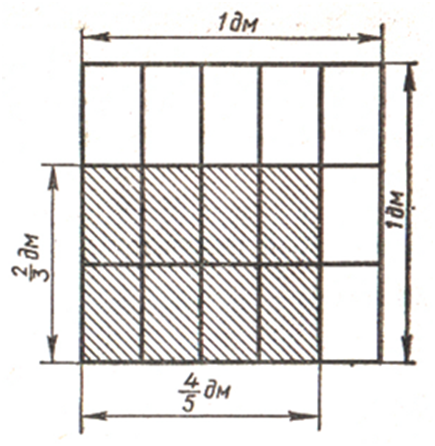
2/3 дм, а ширина 4/5 дм. Найдите площадь прямоугольника.
РЕШЕНИЕ:
квадратный дециметр разделён на 15 (3 ∙ 5 = 15) одинаковых
частей и взято 8 (2 ∙ 4 = 8) таких
частей. Поэтому площадь прямоугольника равна
8/15 дм2. Пользуясь правилом умножения дробей, получим тот же самый
результат:
2/3 ∙ 4/5 = 8/15 (дм2).
ЗАДАЧА:
Площадь прямоугольника равна 5/7 м2, а длина одной его стороны 3/4 м. Найдите длину другой
стороны.
РЕШЕНИЕ:
Обозначим длину другой стороны буквой х. Так
как площадь прямоугольника равна произведению длины на ширину, то произведение 3/4 на х должно быть равно 5/7. Получим
уравнение:
3/4∙ х = 5/7.
Умножив обе части уравнения на число 4/3, обратное
числу 3/4, получим:
4/3 ∙ (3/4 ∙ х) = 5/7 ∙ 4/3,
(4/3 ∙ 3/4) ∙ х = 5/7 ∙ 4/3.
Так как 4/3 ∙ 3/4 = 1,
то х = 5/7 ∙ 4/3,
то есть х = 20/21.
Поэтому, длина другой стороны прямоугольника равна 20/21
м.
ЗАДАЧА:
РЕШЕНИЕ:
Обозначим площадь катка через х. По
условию 2/5 этой площади составляет 800 м2, то есть
2/5 ∙ х = 800.
Чтобы найти х, необходимо
поделить обе две части уравнения на 2/5. Поэтому
х = 800 : 2/5 = 800∙ 5/2 = 2000.
Площадь катка равна
2000 м2.
ЗАДАЧА:
Длина прямоугольника
0,5 дм,
а его ширина 0,3 дм. Найдите площадь прямоугольника.
РЕШЕНИЕ:
Выразим длину и ширину прямоугольника в сантиметрах:
0,5 дм = 5 см,
0,3 дм = 3 см
Площадь этого прямоугольника равна
5 см ∙ 3 см,
то есть равна 15
см2. Так как
1 дм2 = 100 см2, то
1 см2 = 1/100 дм2,
а
15 см2 = 15/100 дм2
= 0,15
дм2.
Если длина и ширина прямоугольника – десятичные дроби, то
его площадь равна произведению длины на ширину. Поэтому и число 0,15 называют произведением
чисел 0,5 и 0,3 и пишут:
0,5 ∙ 0,3 = 0,15.
ОТВЕТ: 0,15 дм2.
ЗАДАЧА:
Длина прямоугольника
4,2 см,
а его ширина 2,8 см. Найдите площадь прямоугольника.
РЕШЕНИЕ:
Выразим длину и ширину прямоугольника в миллиметрах:
4,2 см = 42 мм,
42 мм ∙ 28 мм,
то есть равна 1176 мм2. Так как
1 см2 = 100 мм2, то
1 мм2 = 1/100 см2.
Поэтому
1176 мм2 = 11 см2 76 мм2 =
= 1176/100 дм2
= 11,76
см2.
Значит,
4,2 ∙ 2,8 = 11,76.
Произведение 11,76 можно
найти иначе: умножить
4,2 на 2,5 не обращая внимания на запятые,
и в полученном произведении отделить запятой две цифры справа, то есть столько
же цифр, сколько их после запятой в обоих множителях вместе.
Огород прямоугольной формы длиной 60 м и шириной 45 м разделили на три ровных за площадью грядки. Сколько аров занимает каждая грядка ?
AF = MF = KB = NK.
Необходимо рассмотреть два случая.
1 случай.
20 × 50 = 1000 (см2).
15 × 37,5 = 562,5 (см2).
Задания к уроку 2
- Урок 1. Единицы измерения площади
- Урок 3. Площадь квадрата
- Урок 4. Площадь треугольника
- Урок 5. Площадь прямоугольного треугольника
- Урок 6. Площадь равнобедренного треугольника
- Урок 7. Площадь параллелограмма
- Урок 8. Площадь ромба
- Урок 9. Площадь трапеции
- Урок 10. Площадь равнобедренной трапеции
- Урок 11. Площадь прямругольной трапеции
- Урок 12. Площадь круга и его частей
- Урок 13. Подобие разносторонних треугольников
- Урок 14. Подобие равнобедренных треугольников
- Урок 15. Подобие прямоугольных треугольников
- Урок 16. Площадь многоугольника




Комментариев нет:
Отправить комментарий