суббота, 25 февраля 2017 г.

Урок 22. Преобразование выражений, содержащих степени с отрицательными дробными показателями

Рассмотрим примеры, в которых используются тождественные преобразования выражений, содержащих степени с дробным показателем.

ПРИМЕР:
ПРИМЕР:
Найдите значение выражения:
РЕШЕНИЕ:
ПРИМЕР:
Найдите значение выражения:
РЕШЕНИЕ:
ПРИМЕР:
Найдите значение выражения:
РЕШЕНИЕ:
ПРИМЕР:
Найдите значение выражения:
РЕШЕНИЕ:
ПРИМЕР:
ПРИМЕР:

 Найти  х  из пропорции:

ПРИМЕР:

Упростить выражение:
РЕШЕНИЕ:
ПРИМЕР:

Упростить выражение:
РЕШЕНИЕ:
ОТВЕТ:
ПРИМЕР:

Найти значение выражения при 

х = 12,25:
Предварительно упростим выражение, т. е. преобразуем его в другое, тождественно равное первоначальному на области его определения, но содержащее меньшее число операций:
Равенство:
является тождеством на области определения  первоначального выражения, т. е. на множестве положительных значений  х.
Подставляя в выражение
данное значение  х  и, учитывая, что 

12,25 = 3,52,

получим:
Задания к уроку 22
Другие уроки:
Автор: на

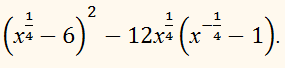
Комментариев нет:

Отправить комментарий

Подписаться на: Комментарии к сообщению (Atom)