понедельник, 13 сентября 2021 г.

Урок 6. Область визначення і область значення тригонометричних функцій

ВІДЕО УРОК

Області визначення тригонометричних функцій.

Будь-яка функція має свою власну сукупність значень аргументу, при яких вона визначена, тобто існує. Ця сукупність всіх допустимих значень аргументу, при яких функція визначена, називається областю визначення або областю існування функції.

Функції  sin α  і  соs α  визначені при будь-якому значенні  α. Справді, будь-яка точка  М, що лежить на одиничному колі, має цілком певні координати  х  і  у, перша з яких є косинус кута  α, складеного з віссю  Ох  рухомим радіусом  ОМ, а друга – синус кута  α.

Функція  tg α  визначена при всіх значеннях  α, за винятком випадку, коли рухомий радіус перпендикулярний до осі  Ох, тобто крім значень  α, рівних

± π/2, ± 3π/2, ± 5π/2, …
і взагалі крім значень α, рівних

 π/2 + kπ,

де  k – будь-яке ціле число.

Справді, при цих (і тільки при цих) значеннях  α  рухомий радіус лежить на осі  Оу, абсциса  х  кінця рухомого радіуса дорівнює нулю (х = 0) і тому ділити у на х не можна.

Функція  сtg α  визначена при всіх значеннях  α, за винятком наступних:

0, ±π, ±2π, ±3π, …
і взагалі – за винятком значень  α, рівних  kπ, де k – будь-яке ціле число, так як при цих (і тільки при цих) значеннях α  рухомий радіус лежить на осі  Ох, ордината у його кінця дорівнює нулю (у = 0) і тому ділити  х  на  у  не можна.

ПРИКЛАД:

Знайдіть область визначення функції

f(x) = tg 2x.

РОЗВ'ЯЗАННЯ:

В область визначення не ввійдуть такі точки:

2х ≠ π/2 + kπ.

або
В результаті отримаємо:

х ≠ π/4 + πk/2, k ∈ Z.

відобразимо графічно.
ВІДПОВІДЬ:

Область визначення функції  tg 2x  всі дійсні числа за винятком

х ≠ π/4 + πk/2, k ∈ Z.

Області значення тригонометричних функцій.

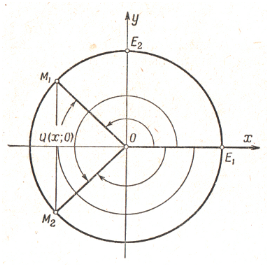
Функції  sin α  і  соs α  приймають всі значення між  –1  і  +1, включаючи і ці числа. Справді, синус кута  α, складеного з віссю  Ох рухомим радіусом  ОМ  одиничному колі, є ордината у точки  М одиничному колі, яка, як легко бачити, приймає всі значення між  –1  і  +1, включаючи і ці числа.
Завдання знаходження кута  α, що має даний синус  у, за умови, що число  у  укладено в межах від  –1  до  +1, має безліч рішень.
 І дійсно, побудуємо на осі  Оу  точку  Р,
ордината якої дорівнює  у, і через цю точку проведемо пряму паралельну осі  Ох. Нехай  М1  і  М2 – точки, в яких ця пряма перетинає одиничну окружність. Якщо позначимо через  α  будь-який кут, складений з віссю  Ох  будь-яким з рухомих радіусів  ОМ1  и  ОМ2, то  sin α = у. На кресленні
відзначено кілька кутів, складених з віссю  Ох  одним з рухомих радіусів  ОМ1  і  ОМ2.

Аналогічно переконуємося в тому, що  соs α  приймає всі значення від –1  до  +1, включаючи і ці числа.

Справді, косинус кута  α, складеного з віссю  Ох  рухомим радіусом ОМ  одиничному колі, є абсциса  х  кінця  М  рухомого радіуса  ОМ, а абсциса  х  точки одиничного кола, приймає всі значення від  –1  до  +1, включаючи і ці числа.
Так само як і для функції  sin α, для заданого числового значення косинуса

соs α = х,

за умови, що число  х  по абсолютній величині не більше одиниці,

–1 ≤ х ≤  +1,

існує безліч кутів, косинус яких дорівнює  х.

І дійсно, побудуємо на осі  Ох  точку  Q, абсциса якої дорівнює  х, і провівши через цю точку пряму, паралельну осі  Оу. Нехай  М1  і  М2 – точки, в яких ця пряма перетинає одиничну окружність. Якщо через  α  ми позначимо будь-який кут, складений з віссю  Ох  будь-яким з рухомих радіусів  ОМ1  або  ОМ2, то  соs α = х.

На кресленні
відзначено кілька кутів, складених з віссю  Ох  одним з рухомих радіусів  ОМ1  або  ОМ2.
 На кресленні
ми взяли  0 < у < 1.
 На кресленні
ми беремо

–1 < х < 0.

Функція  tg α  приймає всі дійсні значення. Справді, нехай  р – будь-яке дійсне число. Доведемо, що існує і притом безліч кутів, тангенси яких дорівнюють  р.

Побудуємо на осі тангенсів точку  р,

ордината якої дорівнює  р. З'єднаємо точку  Р  з початком координат і продовжимо  РО  за центр до перетину з одиничною окружністю. Нехай  М1  і  М2 – точки, в яких пряма  РО  перетинає коло. Тоді, якщо  α – кут, складений з віссю  Ох  будь-яким з рухомих радіусів  ОМ1  або  ОМ2, то

tg α = р.

На кресленні

ми вважали, що  р ˃ 0. На цьому ж кресленні зазначено кілька кутів, складених з віссю  Ох  радіусами  ОМ1  або  ОМ2. Тангенси всіх цих кутів рівні  р.

Нарешті, функція  сtg α, як і  tg α, приймає всі дійсні значення.

Справді, нехай  q – будь-яке число. Побудуємо на осі котангенсів точку  Q, абсциса якої дорівнює  q, з'єднаємо цю точку  Q  з початком координат і продовжимо  QО  за центр до перетину з одиничною окружністю.
Позначимо через  М1  і  М2  точки перетину прямої  QО  з одиничною окружністю. Тоді котангенс будь-якого з кутів, складених з віссю  Ох  радіусом  ОМ1  або  ОМ2, буде дорівнює  q.

ПРИКЛАД:

Знайти область значень функції:

у = 5 – 4 sin х.

РОЗВ'ЯЗАННЯ:

З визначення синуса слід,

–1 ≤ sin х ≤ 1.

Далі скористаємося властивостями числових нерівностей.

Помножимо всі три частини подвійного нерівності на  –4.

–4 ≤ –4 sin х ≤ 4.

Додамо до трьох частин подвійного нерівності  5.

1 ≤ 5 – 4 sin х ≤ 9.

Так як дана функція неперервна на всій області визначення, то безліч її значень укладено між найменшим і найбільшим її значенням на всій області визначення, якщо такі існують. В даному випадку безліч значень функції

у = 5 – 4 sin х

є безліч  [1; 9].

ВІДПОВІДЬ:  [1; 9]

ПРИКЛАД:

Знайти область визначення і область значень функції:

y = tg x.

РОЗВ'ЯЗАННЯ:

Функція  y = tg x  визначається формулою
Ця функція визначена при значеннях  х, для яких  соs х ≠ 0.

Відомо, що  соs х = 0  при

х = π/2 + πn, n ∈ Z.

Отже, областю визначення функції  y = tg x  є безліч чисел крім

х = π/2 + πn, n ∈ Z.

Так як рівняння  tg x = а  має коріння при будь-якому дійсному значенні  а, то безліччю значень функції  y = tg x  є безліч  R  всіх дійсних чисел.

ПРИКЛАД:

Знайти область визначення функції:

y = sin 3х + tg 2x.

РОЗВ'ЯЗАННЯ:

Потрібно з'ясувати, при яких значеннях  х  вираз

y = sin х + tg 2x

має сенс. Вираз  sin 3х  має сенс при будь-якому значенні  х, а вираз tg 2x – при всіх значеннях  х  окрім

2х = π/2 + πn, n ∈ Z  або

х = π/4 + πn/2, n ∈ Z.

Отже, областю визначення даної функції є безліч дійсних чисел, крім

х = π/4 + πn/2, n ∈ Z.

ПРИКЛАД:

Знайти область значення тригонометричної функції:

у = 3 соs х – 2.

РОЗВ'ЯЗАННЯ:

Для знаходження області значення функції

у = 3 соs х – 2

використовуємо той факт, що функція  у = соs х  змінює своє значення від  –1  до  1, тобто має місце подвійне нерівність:

–1 ≤ соs х ≤ 1.

Помножимо всі частини цієї нерівності на  3:

–3 ≤ 3 соs х ≤ 3.

Віднімемо з усіх частин отриманого нерівності  2, отримаємо:

–3 – 2 ≤ 3 соs х – 2 ≤ 3 – 2,

–5 ≤ 3 соs х – 2 ≤ 1.

Таким чином, область значень функції буде проміжок

[–5; 1].

ВІДПОВІДЬ:  [–5; 1]

ПРИКЛАД:

Знайти область значення тригонометричної функції:

у = 3 соs х – 4 sin х.

РОЗВ'ЯЗАННЯ:

Для знаходження області значення функції

у = 3 соs х – 4 sin х

скористаємося наступною формулою:
У нашому випадку  а = 3, b = –4, тобто:
Отже, областю значень є проміжок:

[–5; 5].

ВІДПОВІДЬ:  [–5; 5]

Завдання до уроку 6

Інші уроки:
Автор: на

Комментариев нет:

Отправить комментарий

Подписаться на: Комментарии к сообщению (Atom)