Всякая
функциональная связь между двумя величинами может быть изображена плоскостным
графиком.
Пусть функция задана аналитически формулой у = f(х). Если на координатной
плоскости отметить все точки, обладающие следующим свойством: абсцисса точки
принадлежит области определения функции, а ордината равна соответствующему
значению функции – то получится множество точек
(х; f(х)) – график функции.
Графиком функции называется множество всех точек
координатной плоскости, абсциссы которых равны значению аргумента, а ординаты –
соответствующим значениям функции.
Наипростейший способ
построения графика функции – по точкам.
На практике для построения графика функции
составляют таблицу значений функции при некоторых значениях аргумента, наносят
на плоскость соответствующие точки и соединяют полученные точки линией. При
этом предполагают, что найденные точки достаточно точно показывают ход
изменения функции.
Возьмём какую-нибудь функцию у =
f(х). Что бы построить график
функции, прежде всего надо, пользуясь данной формулой, составить таблицу, в
которой записать значения Х и соответственно
значения Y. Обозначим значения аргумента на оси абсцисс, и
соответствующие значения функции – длиною перпендикуляра, проведённого до оси
абсцисс с этой точки. Затем на координатную
плоскость нанести полученные точки и их плавно соединить.
Тогда при возможных
изменениях аргумента концы перпендикуляров образуют некоторое множество точек, которое
называется графиком данной функции. Часто графиком функции будет некоторая линия.
Однако он может состоять из отдельных точек, отрезков, дуг и т. д..
Если функция задана
графиком, то можно легко определить для каждого (допустимого) значения аргумента
соответствующее значение функции. Для этого достаточно поставить в соответствующей
точке оси абсцисс перпендикуляр к ней и продолжить его до пересечения с графиком.
Ордината точки пересечения и даёт соответствующее значение функции.
Имея график
функции, можно для любого значения аргумента (из области определения) указать
соответствующее значение функции. Или наоборот, пользуясь графиком, можно
составить таблицу значений функции. На графике промежутки существования функции
обозначаются утолщением оси абсцисс, причём замкнутый конец промежутка
обозначается точкой, а открытый конец (не включённый в область существования) –
кружком, стрелкой или совсем не обозначаются. Графический способ задания
функции удобен своею наглядностью. Смотря на график, сразу же можно определить
свойства функции, которую он задаёт.
Совокупность всех точек числовой оси, заключённых
между двумя какими-нибудь точками этой оси, называется промежутком.
Крайние точки промежутка называются концами промежутка.
Промежуток со
включением его концов называется замкнутым или закрытым промежутком,
а также отрезком или сегментом. Обозначается:
от
–1 до +1 или [–1;
1].
Промежуток без
включения его концов называется открытым промежутком или интервалом.
Обозначается:
(–1; 1).
Если один конец
присоединяется к промежутку, а другой нет, то такой промежуток, открытый с
одной стороны и закрытый с другой, называется полуоткрытым промежутком или
полуинтервалом.
Обозначается:
(–1; 1] или
[–1; 1).
ПРИМЕР:
Пусть функция f задана таблицей:
Выпишем пары соответственных значений переменных х и у:
(–2; 2), (–1; 1),
(0; 0), (1; –1), (2; 0),
(3; 1), (4; 2).
Начертим оси координат: ось х,
обычно называемую осью абсцисс,
и ось у,
называемую осью ординат. Построим на
координатной плоскости точки, координатами которых служат выписанные пары чисел
(первая координата точки – абсцисса,
вторая координата точки – ордината). Множество построенных точек называют графиком функции
f.
Тогда можно сказать, что между множеством
X =
{–2; –1; 0; 1; 2; 3; 4}
и множеством
Y =
{2; 1; 0; –1; 0; 1; 2}
с помощью графика задано соответствие.
ПРИМЕР:
Построить график функции
у = х2.
РЕШЕНИЕ:
(0: 0), (0,5: 0,25), (–0,5: 0,25), (1: 1),
(–1: 1), (2: 4), (–2: 04), (3: 9), (–3: 9).
ПРИМЕР:
Постройте график функции:
у = х2
– 2.
Для этого вычислим значения функции для нескольких значений
аргумента, например для
–3, –2,
–1, 0, 1,
2, 3.
Результаты удобно записать в виде таблицы.
у =
х2 – 2.
Можно ли по виду
графика узнать, является ли заданное им соответствие функцией ?
Если на графике нет
точек с одинаковыми абсциссами, т. е. если каждой абсциссе соответствует
единственная ордината, то соответствие, заданное графиком, является функцией.
ПРИМЕР:
Кривая АВ служит графиком соответствия между множеством
X =
[1; 5]
и множеством
Y =
[1; 4]
ПРИМЕР:
Кривая CD служит графиком соответствия между множеством
X =
[2; 6]
и множеством
Y =
[1; 4].
ПРИМЕР:
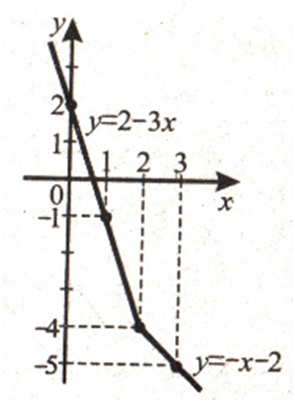
Запишем функцию в следующем видеИли,При х ≥ 2 построим часть прямой, которая проходит через точки
(2; –4) и (3; –5).
При х < 2: часть прямой, которая
проходит через точки
Запишем функцию в следующем видеИли,
При х ≥ 0 построим часть прямой, которая проходит через точки
(0; 0) и (1; –1).
При х < 0: часть прямой, которая
проходит через точки
Другие уроки:
- Урок 1. Координатная плоскость
- Урок 2. Диаграммы
- Урок 3. Графики
- Урок 4. Множества
- Урок 5. Что такое функция ?
- Урок 6. Аналитический способ задания функции
- Урок 7. Табличный способ задания функции
- Урок 9. Нахождение области определения и области значения функции аналитическим методом
- Урок 10. Нахождение области определения и области значения функции с помощью графика
- Урок 11. Нули функции
- Урок 12. Возрастание и убывание функции
- Урок 13. Экстремальные значения функции
- Урок 14. Симметричные функции
- Урок 15. Чётные и нечётные функции
- Урок 16. Функция, обратная данной
- Урок 17. Линейная функция
- Урок 18. График линейной функции
- Урок 19. Прямая пропорциональность
- Урок 20. График прямой пропорциональности
- Урок 21. Взаимное расположение графиков линейных функций
- Урок 22. Функция обратно пропорциональной зависимости
- Урок 23. График функции обратно пропорциональной зависимости
- Урок 24. Квадратичная функция
- Урок 25. График функции у = aх2 + b
- Урок 26. График функции у = a(х - m)2 + n
- Урок 27. График функции у = aх2 + bx + c
- Урок 28. Функция y = √͞͞͞͞͞х и её график
- Урок 29. Функция y = хn и её график
- Урок 30. Построение графиков функций методом геометрических преобразований
















Комментариев нет:
Отправить комментарий