четверг, 20 июля 2017 г.

Урок 22. Функция обратно пропорциональной зависимости

Обратная пропорциональность представляет собой зависимость функции, при которой изменение независимой величины (аргумента) влечёт пропорциональное изменение зависимой величины (функции).

Другими словами, во сколько раз увеличивается аргумент, во столько же раз уменьшается функция, и, наоборот, во сколько раз уменьшается аргумент, во столько же раз увеличивается функция.

Зависимость между величинами  х  и  у, которую можно выразить формулой
где  k – некоторое заданное число, называют
обратно пропорциональной зависимостью.
Здесь 

k, х, у 

могут быть не только положительными числами, но и отрицательными. Поэтому приведённое здесь определение более общее, чем давалось раньше.
Эта функция называется равносторонней гиперболой.

Свойства обратно пропорциональной функции.

 – область определения – все действительные числа, кроме значения  х, равного нулю, то есть промежуток

D(–∞; 0) ∪ D(0; + ∞);

– множество значений – все числа, исключая  у = 0, то есть

Е(–∞; 0) ∪ Е(0; + ∞);

– у функции отсутствуют максимальное и минимальное значения;

– функция нечётная, её график симметричен по отношению к точке  (0; 0), то есть началу координат;
– функция неповторяющаяся, следовательно, не является периодической;

– график не пересекает оси абсцисс и ординат;

– функция не имеет нулей;

– при  k ˃ 0  у функции  у = k/x   на промежутках от  –∞  до  0  и от  0  до  +∞  наблюдается возрастание;

– функция у = k/x  (k ˃ 0) на промежутке от  –∞  до  0  отрицательна, а на участке от  0  до  +∞ – положительна;

– функция у = k/x  (k < 0) на участке  (0; + ∞) – меньше нуля, а на промежутке  (–∞; 0) – больше нуля.

ПРИМЕР:

Укажите, какую из функций можно назвать обратной пропорциональностью.
РЕШЕНИЕ:
Так как функция обратной пропорциональности выглядит в виде дроби, в которой аргумент  х  обязательно должен быть в знаменателе, то это будут следующие дроби:
Задачи, приводящие к понятию обратной пропорциональности.

ЗАДАЧА:

Площадь прямоугольника со сторонами  х  и  у  равна  S. Выразите  у  через  S  и  х.

РЕШЕНИЕ:

Площадь прямоугольника выражается формулой  S = ху.

Выразим  у  через  S  и  х:  у = S/х.

Если  S = 6,  то  у = 6/х.

Подставим вместо  х  следующие числа, которые указаны в таблице, и найдём  у.
Из таблицы видно, что при увеличении  х  в несколько раз, у  уменьшается в такое же количество раз.

ЗАДАЧА:

Площадь прямоугольника со сторонами  х  и  у  равна  S. Выразите  у  через  S  и  х.

РЕШЕНИЕ:

Площадь прямоугольника выражается формулой  S = ху.

Выразим  у  через  S  и  х:  у = S/х.

Если  S = 24,  то  у = 24/х.

Подставим вместо  х  следующие числа, которые указаны в таблице, и найдём  у.
Из таблицы видно, что при увеличении  х  в несколько раз, у  уменьшается в такое же количество раз.

ЗАДАЧА:

Пешеход путь  S  проходит со скоростью  v  за  t  часов. Выразите время пешехода через путь и скорость.

РЕШЕНИЕ:

Расстояние, пройденное пешеходом,  выражается следующей формулой  S = vt.

Выразим  t  через  S  и  v:  t = S/v.

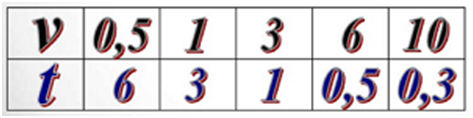
Если  S = 3,  то  t = 3/v.

Подставим вместо  v  следующие числа, которые указаны в таблице, и найдём  t.
Из таблицы видно, что при увеличении  v  в несколько раз, t  уменьшается в такое же количество раз.

ЗАДАЧА:

Пешеход путь  S  проходит со скоростью  v  за  t  часов. Выразите время пешехода через путь и скорость.

РЕШЕНИЕ:

Расстояние, пройденное пешеходом,  выражается следующей формулой  S = vt.

Выразим  t  через  S  и  v:  t = S/v.

Если  S = 60,  то  t = 60/v.

Подставим вместо  v  следующие числа, которые указаны в таблице, и найдём  t.
Из таблицы видно, что при увеличении  v  в несколько раз, t  уменьшается в такое же количество раз.

Задания к уроку 22
Другие уроки:
Автор: на

Комментариев нет:

Отправить комментарий

Подписаться на: Комментарии к сообщению (Atom)