(5х – 4) × 7 = (16х + 1) × 2;
ПРИКЛАД:
Розв’яжемо
рівняння
0,1х = –8.
РОЗВ'ЯЗАННЯ:
Наведемо
рівняння до цілого виду поділивши обидві частини рівняння на
0,1, матимемо, що
х = –8 : 0,1,
х = – 80.
Той
самий результат можна дістати, якщо помножити обидві частини рівняння на 10.
ПРИКЛАД:
Знайдіть
значення змінної х, при якому значення виразу
2х – 5
і 2
– 1,5х
рівні.
РОЗВ'ЯЗАННЯ:
2х – 5 =
2 – 1,5х,
3,5х = 7,
х = 2.
ПРИКЛАД:
Розв’яжіть
рівняння:
4(х – 1,5) = 6.
РОЗВ'ЯЗАННЯ:
4(х – 1,5) = 6,
4х – 6 = 6,
4х = 12,
4х = 3.
ПРИКЛАД:
Наведемо
рівняння до цілого виду.
Це
рівняння рівносильне рівнянню
х – 1 = 6х
(обидві частини першого рівняння помножили на 3).
х – 1 = 6х,
5х = –1,
х
= –0,2.
ПРИКЛАД:
Наведемо
рівняння до цілого виду.
Помножимо
ліву та праву частини на 4, отримаємо
3х = 48.
Розділимо
ліву та праву частину рівняння на 3:
х = 16.
ВІДПОВІДЬ:
х
= 16
ПРИКЛАД:
3(х – 1) = 2(2х + 4).
Розкриємо
дужки:
3х – 3 = 4х + 8.
Згрупуємо
в одній частині члени, які містять невідомі, а в іншій – вільні члени:
3х – 4х
= 8 + 3.
Наведемо
подобні членів:
–
х = 11, х =
–11.
ВІДПОВІДЬ: –11
ПРИКЛАД:
5(5х – 1) – 3(2х + 3) = 15.
Розкриємо
дужки:
25х – 5 – 6х – 9 = 15.
Згрупуємо
в одній частині члени, які містять невідомі, а в іншій – вільні члени:
25х – 6х
= 15 + 5 + 9.
Наведемо
подобні членів:
19х = 29,
х
= 29/19
= 110/19.
ВІДПОВІДЬ: 110/19
ПРИКЛАД:
3(3х – 4) = 4 ∙ 7х + 24.
Розкриємо
дужки:
9х – 12 = 28х + 24.
Згрупуємо
в одній частині члени, які містять невідомі, а в іншій – вільні члени:
9х – 28х = 24 + 12.
Наведемо
подобні членів:
–19х = 36,
х
= –36/19
= –117/19.
- Урок 1. Лінійне рівняння з одним невідомим і цілими вільними членами
- Урок 3. Застосування правил визначення невідомого доданка, зменшуваного і від'ємника для розв'язання задач
- Урок 4. Застосування правил визначення невідомого множника для розв'язання задач
- Урок 5. Розв'язування рівнянь, що зводяться до лінійних
- Урок 6. Розв'язування рівнянь із змінною в знаменнику
- Урок 7. Застосування правил визначення діленого і дільника для розв'язання задач
- Урок 8. Лінійне рівняння з двома невідомими
- Урок 9. Рішення лінійних рівнянь за допомогою графіків
- Урок 10. Лінійне рівняння з параметром
- Урок 11. Системи двох рівнянь першого степеня з двома невідомими
- Урок 12. Розв'язання систем рівнянь способом підстановки
- Урок 13. Розв'язання систем рівнянь способом алгебраїчного додавання
- Урок 14. Рішення лінійних систем рівнянь за допомогою графіків
- Урок 15. Розв'язування задач за допомогою систем лінійних рівнянь
- Урок 16. Системи трьох лінійних рівнянь з трьома невідомими
- Урок 17. Повне квадратне рівняння загального вигляду
- Урок 18. Зведене квадратне рівняння
- Урок 19. Теорема Вієта
- Урок 20. Неповні квадратні рівняння
- Урок 21. Розв'язання квадратного рівняння способом виділення квадрата двочлена
- Урок 22. Графічний спосіб розв'язування квадратних рівнянь
- Урок 23. Квадратний тричлен
- Урок 24. Квадратні рівняння з параметрами
- Урок 25. Дробові раціональні рівняння
- Урок 26. Задачі на складання квадратних рівнянь
- Урок 27. Рівняння кола
- Урок 28. Системи рівнянь другого степеня є двома невідомими
- Урок 29. Розв'язування задач за допомогою систем рівнянь другого степеня
- Урок 30. Перетин прямої з колом
- Урок 31. Рішення нелінійних систем рівнянь за допомогою графіків
- Урок 32. Системи рівнянь з параметрами
- Урок 33. Рівняння вищих степенів
- Урок 34. Розв'язання рівнянь способом заміни
- Урок 35. Розв'язання систем рівнянь способом заміни
- Урок 36. Задачі на знаходження чисел
- Урок 37. Задачі на знаходження цифр
- Урок 38. Рішення задач на змішування за допомогою рівнянь
- Урок 39. Рішення задач на змішування за допомогою систем рівнянь
- Урок 40. Ірраціональні рівняння



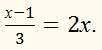







Комментариев нет:
Отправить комментарий